2015-08-12
213
Рассмотрим задачу: монету подбрасывают 200 раз. Необходимо вычислить вероятность появления герба в 90 испытаниях. Применим формулу Бернулли:
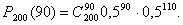
Видим, что вычислить по данной формуле требуемую вероятность довольно сложно из-за громоздких вычислений. Рассмотрим методы вычислений, дающие возможность с довольно высокой точностью найти вероятность в подобных случаях. Первый из них описан в теореме Муавра- Лапласа. Эта теорема дает приближенную формулу для вычисления вероятности появления события А в схеме повторных испытаний, когда нужно вычислить появление события А ровно т раз из п испытаний.
Теорема Муавра- Лапласа: Если вероятность наступления события А в каждом из п независимых испытаниях равна р и отлична от 0 и единицы, а число испытаний достаточно велико, то вероятность Рп(т)того, что в п испытаниях событие А наступит т раз, приближенно равна значению функции
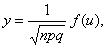
где
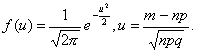
Значение функции f(u)(или j(х)) можно найти в "Таблице значений функции j(х)". При этом нужно учитывать, что функция четная. При u>4 значение функции принимается равным нулю.
|
|
|
ИНТЕГРАЛЬНАЯ
Вернемся к предыдущей задаче, но изменим вопрос. Пусть требуется вычислить вероятность того, что попаданий по мишени будет не менее 50 и не более 70.
Вычислить вероятность для каждого случая конечно можно. Используя рассмотренный метод, но диапазон довольно велик, поэтому на практике в подобных случаях для расчетов применяют формулу, позволяющую вычислить вероятность для любого диапазона (т1, т2). Эту формулу дает интегральная теорема Муавра- Лапласа.
Интегральная теорема Муавра- Лапласа: Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность Рп(т1, т2) того, что событие А появится в п испытаниях от т1 до т2 раз. Приближенно равна определенному интегралу
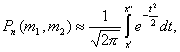где
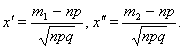
Данный интеграл называется функцией Лапласа и обозначается Ф(х).
Ф(х)- нечетная функция, значения ее приведены в "Таблице значений функции Ф(х)". При x>5 принимают Ф(х)=0,5.
Вернемся к задаче и вычислим требуемую вероятность:
33. Интервальные оценки параметров распределения. Доверительный интервал для математического ожидания нормальной генеральной совокупности
Интервальные оценки параметров распределения.
Интервальной называют оценку, которая определяется двумя числами—концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.
Пусть найденная по данным выборки статистическая характеристика Q* служит оценкой неизвестного параметра Q. Будем считать Q постоянным числом (Q может быть и случайной величиной). Ясно, что Q* тем точнее определяет параметр Q, чем меньше абсолютная величина разности |Q- Q*|. Другими словами, если d>0 и |Q- Q*| <d, то чем меньше d, тем оценка точнее.
|
|
|
Таким образом, положительное число d характеризует точность оценки.
Однако статистические методы не позволяют категорически утверждать, что оценка Q* удовлетворяет неравенству |Q- Q*| <d; можно лишь говорить о вероятности g, с которой это неравенство осуществляется.
Надежностью (доверительной вероятностью) оценки называют вероятность g, с которой осуществляется неравенство |Q—Q* | <d.
Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.
Пусть вероятность того, что, |Q- Q*| <d равна g:
P(|Q- Q*| <d)= g.
Заменив неравенство равносильным ему двойным неравенством получим:
Р [Q* —d< Q < Q* +d] = g
Это соотношение следует понимать так: вероятность того, что интервал Q* - d< Q < Q* +d заключает в себе (покрывает) неизвестный параметр Q, равна g.
Интервал (Q* - d Q* +d) называется доверительным интервалом, который покрывает неизвестный параметр с надежностью g.
