Распределения случайных величин и функции распределения
Распределение числовой случайной величины – это функция, которая однозначно определяет вероятность того, что случайная величина принимает заданное значение или принадлежит к некоторому заданному интервалу.
Первое – если случайная величина принимает конечное число значений. Тогда распределение задается функцией Р(Х = х), ставящей каждому возможному значению х случайной величины Х вероятность того, что Х = х.
Второе – если случайная величина принимает бесконечно много значений. Это возможно лишь тогда, когда вероятностное пространство, на котором определена случайная величина, состоит из бесконечного числа элементарных событий. Тогда распределение задается набором вероятностей P(a <X <b) для всех пар чисел a, b таких, что a<b. Распределение может быть задано с помощью т.н. функции распределения F(x) = P(X<x), определяющей для всех действительных х вероятность того, что случайная величина Х принимает значения, меньшие х. Ясно, что
P(a <X <b) = F(b) – F(a).
Это соотношение показывает, что как распределение может быть рассчитано по функции распределения, так и, наоборот, функция распределения – по распределению.
Используемые в прикладных исследованиях функции распределения бывают либо дискретными, либо непрерывными, либо их комбинациями.
Дискретные функции распределения соответствуют дискретным случайным величинам, принимающим конечное число значений или же значения из множества, элементы которого можно перенумеровать натуральными числами (такие множества в математике называют счетными).
Свойства функций распределения.
Функцией распределения случайной величины мы назвали функцию. Основные свойства этой функции заключены в теореме:
15.4.1 Индикатор случайного события (случайная величина Бернулли) - это случайная величина, заданная таблицей:
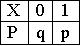 q= 1 -p, где q и p - константы
q= 1 -p, где q и p - константы
Пусть ( 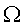 , P) - вероятностное пространство, А -событие, P (A) = p
, P) - вероятностное пространство, А -событие, P (A) = p
Рассмотрим случайную величину:
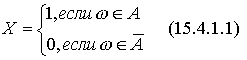
Теорема 15.4.1 Случайная величина Х, определенная равенством (15.4.1.1) является индикатором случайного события.
Д о к а з а т е л ь с т в о
Составим таблицу.
P (X= 1) = P (A) = p
P (X= 0) = P ( 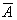 ) = 1 -P (A) = 1 -p = q, т.е. таблица имеет вид
) = 1 -P (A) = 1 -p = q, т.е. таблица имеет вид

Если Х - индикатор случайного события, то это обозначается так:
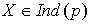
28. Локальная и Интегральная теоремы Муавра- Лапласа.
 2015-08-12
2015-08-12 238
238







