Составление двойственных задач

Симплекс-метод. Метод обратной матрицы.

Задание 1. Решить задачу методом обратной матрицы.

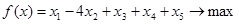
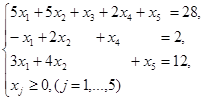
Решение:

1)

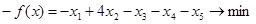
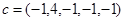
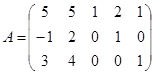
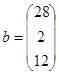
2) Выберем первоначальную базисную матрицу .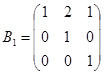

Найдем ее определитель 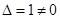. 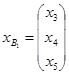- вектор базисных переменных. .

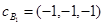Тогда, небазисная матрица 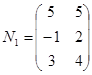. 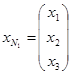- вектор небазисных переменных. .

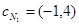3) .

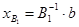4) Найдем обратную матрицу к матрице .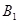

. .

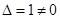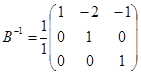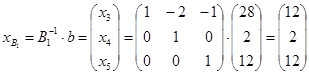
5) Найдем вектор .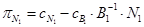

.

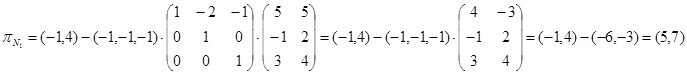6) Так как каждая из координат вектора 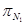положительна, то последнее найденное решение 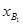является оптимальным, 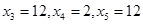или (0,0,12,2,12). .

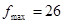Составление двойственных задач.

Задание 1. Является ли вектор 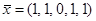оптимальным планом задачи.

1. Составляем двойственную задачу:

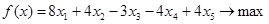
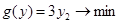
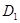
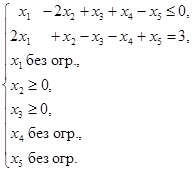
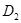
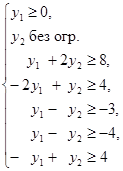
2. Непосредственной подстановкой убедимся в том, что .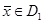

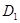
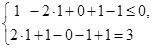
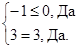
3. После этого проверим план 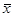на оптимальность. Для этого запишем систему характеристических произведений для вектора 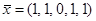и .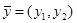

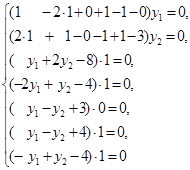
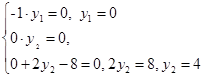Из 2-го уравнения ничего нельзя сказать о .

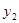4. Итак, 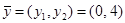совместно с вектором 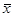зануляют все характеристические произведения.

5. Осталось проверить, что .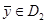

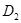
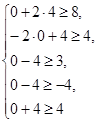
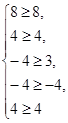не является верным

3 условие не выполняется, поэтому 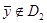, следовательно и план 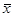не оптимален.

Замечание: Если мы нашли, например, с помощью табличного симплекс-метода, оптимальный план одной из пары двойственных задач, то для нахождения оптимального плана другой задачи нет необходимости решать ее симплекс-методом. Достаточно применить вторую теорему двойственности, то есть составить и решить систему характеристических произведений.