2015-08-21
265
Розглянемо рішення задачі про стаціонарні автоколивання квазілінійних систем, диференціальне рівняння руху яких має вигляд:
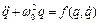. (6.3)
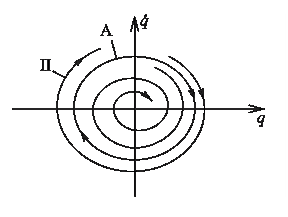
Рисунок 6.3 – Фазовий портрет автоколивань
з нестійким граничним циклом
Нехай функція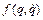 
складається з малих нелінійних членів. Тоді можна прийняти, що частота автоколивань дорівнює власній частоті 
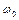системи і шукати розв’язко у вигляді
,
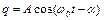де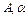 
- постійні величини.
У відповідності з ідеєю методу енергетичного балансу (3.2) вимагатимемо, щоб робота «неврівноваженої сили»,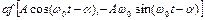 
(тут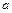 
– інерційний коефіцієнт рівняння) за період 
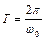дорівнювала нулю. Умова енергетичного балансу дає вираз для визначення стаціонарної амплітуди автоколивань:
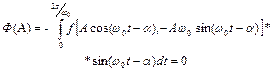, (6.4)
де введемо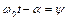 
.
Розглянемо приклад автоколивальної системи зі звичайною силою в'язкого тертя і силою негативного кулонівського тертя (рис. 6.4), яка і є причиною самозбудження коливань.
Диференціальне рівняння руху має вигляд
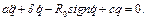
Функція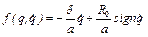 
або
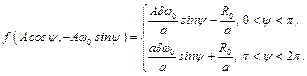
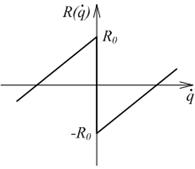
Рисунок 6.4 – Характеристика сили тертя
Умова (6.4) тепер дає
,
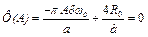звідки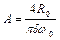 
.
КОНТРОЛЬНІ ЗАПИТАННЯ І ЗАВДАННЯ ДО РОЗДІЛУ 6
1. Поясніть принципову відмінність автоколивальних систем від розглянутих раніше.
2. Що означає стійкий і нестійкий граничні цикли?
3. Чи можливе існування декількох граничніх циклів? Від чого це залежить?
4. Як впливають початкові збурення на коливання в автогенераторі Ван-дер-Поля?
7 КОЛИВАННЯ У ВПОРЯДКОВАНИХ СТРУКТУРАХ.
ХВИЛЬОВЕ РІВНЯННЯ
