Симплекс-метод, известный также в нашей литературе под названием метода последовательного улучшения плана, впервые разработал Г.Данциг в 1947 г. Этот метод позволяет переходить от одного допустимого базисного решения к другому, причем так, что значения целевой функции непрерывно возрастают. В результате оптимальное решение находят за конечное число шагов.
Алгоритмы симплекса-метода позволяют также установить, является ли задача ЛП разрешимой.
Запишем ограничения задачи ЛП в таком виде:
A 1 x 1 + A 2 x 2 + … + A nxn + A n +1 xn +1 +…+ A n + m xn + m = A 0.
Пусть A 1,…, A m –множество линейно независимых векторов.
Тогда уравнение
A 1 x 1*+ A 2 x 2* + … + A nxn * + A n +1 xn +1* +…+ A n + m xn + m * = A 0, (2...2.1)
определяет базисное решение x 1 *, x 2 *,…,xm *,
Предположим, что это решение допустимо, то есть x 1*³0, x 2*³0 ,…, xm *³0. Базис { A 1,…, A m }образует m –мерное пространство, а потому каждый из векторов A m +1,…, A m + n единственным образом выражается через этот базис. Если A r не входит в базис, то
A 1 x 1 r + A 2 x 2 r + … + A mxmr = A r, (2...2.2)
где xir – соответствующие коэффициенты (i = 1, 2,..., m).
Предположим, что хотя бы одна из величин xir больше нуля.
Решение уравнения
A 1 x 1 + A 2 x 2+ … + A mxm + A rxr = A 0 (2...2.3)
обозначим как 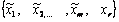
Тогда,очевидно:
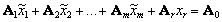 . (2.2.4)
. (2.2.4)
Умножив уравнение (2.2.2) на xr и вычтя полученное уравнение из уравнения (2.2.1), получим
A 1(x 1*– xrx 1 r ) + A 2(x 2*– xrx 2r) +…+ A m (xm *– xrxmr)= A 0– xr A r. (2.2.5)
Сравнив уравнения (2.2.5) и (2.2.4), находим связь нового решения 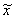 1,…,
1,…, 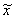 m, xr со старым базисным решением x* 1,…, x*m:
m, xr со старым базисным решением x* 1,…, x*m:
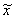 1= x 1*– xrx 1 r ,
1= x 1*– xrx 1 r , 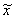 2= x 2*– xrx 2 r ,…,
2= x 2*– xrx 2 r ,…, 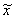 m = xm *– xrxmr , xr. (2.2.6)
m = xm *– xrxmr , xr. (2.2.6)
Решение (2.2.6), во-первых, не будет базисным, так как содержит
m + 1 переменную, а во-вторых, будет допустимым не для всех значений xr.
Чтобы новое решение оставалось допустимым, нужно выбрать значение xr таким, чтобы ни одна из величин 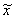 i = xi* – xrxir (i= 1, 2,..., m) не стала меньше нуля. Следовательно, максимальное значение переменной xr определяется соотношением
i = xi* – xrxir (i= 1, 2,..., m) не стала меньше нуля. Следовательно, максимальное значение переменной xr определяется соотношением
x r max = 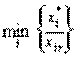 , (2.2.7)
, (2.2.7)
где xir > 0.
Чтобы сделать новое допустимое решение базисным, нужно одну переменную xi вывести из базисного решения, а соответствующий вектор из базиса. В этом случае новый базис будет содержать также m векторов.
Для этого выбираем значения в соответствии с (2.2.7). Тогда новое базисное решение имеет вид
x 1* – xr max x 1 r ;
x 2* – xr max x 2 r ;
xj (опущен)
xr max,
а новый базис – (A 1, A 2, …, A j -1, A j +1, …, A m, A r).
Такой переход от одного базиса к другому позволяет находить решения почти всех задач ЛП. Определив все крайние точки, можно вычислить значения целевой функции и найти оптимальное решение. Однако для больших значений m и n это практически невозможно. Поэтому для перехода от текущего решения к новому допустимому базисному решению, которому отвечает большее значение целевой функции, используют соответствующий критерий (симплекс-разность).
Новому ДБР { x 1* – xrx 1 r , x 2* – xrx 2 r , …, xm * – xrxmr, xr }
соответствует следующее значение целевой функции
z 1 = с 1(x 1*– xrx 1 r ) + с 2(x 2*– xrx 2r) +…+ сrxr =
= (с 1 x 1*+ с 2 x 2*+…+ сmxm *)+ xr (сr – с 1 x 1 r –…– сmxmr)=
= z 0+ xr (сr – с 1 x 1 r –…– сmxmr), (2.2.8)
где z0 – значение целевой функции для начального ДБР;
сr – с 1 x 1 r – с 2 x 2 r – … – сmxmr – симплекс-разность для переменной хr.
Симплекс-разность вычисляют для каждой переменной, не входящей в базисное решение, и выбирают такую небазисную переменную хr, для которой симплекс-разность положительна и максимальна.
Таким образом, алгоритм симплекса-метода состоит из следующих этапов:
1) находят начальный базис и связанное с ним допустимое базисное решение;
2) вычисляют симплекс-разность для каждой переменной, не входящей в базисное решение;
3) вводят в базис наиболее “выгодную” переменную с максимальной положительной симплексом-разностью; ее значение xrmax определяют из соотношения
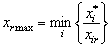

для всех xir > 0,
4) выводят из базисного решения переменную xj, соответствующую

а из базиса – вектор A j;
5) переходят к этапу 2 новой итерации.
Этапы 2) - 4) повторяют до тех пор, пока симплекс-разности для всех переменных, не входящих в базис, не станут отрицательными.
Это и есть признак оптимальности текущего базисного решения.
Пример 2.2. Решить симплексом-методом такую задачу:
максимизировать (2 x 1+5 x 2)
при ограничениях
x 1£400, x 2£300, x 1+ x 2£500.
Расширенная форма задачи имеет вид

Ограничения задачи запишем в виде табл. 2.1.
Первая итерация. 1. Выбрав в качестве начального базиса векторы { A 3, A 4, A 5}, находим первое допустимое базисное решение:
A 3 x 3*+ A 4 x 4*+ A 5 x 5*= A 0,
откуда x 3*=400, x 4*=300, x 5*=500,
2. Записываем каждый из небазисных векторов A 1, A 2 в виде линейной комбинации базисных { A 3, A 4, A 5}
A 3 x 31+ A 4 x 41+ A 5 x 51= A 1;
A 3 x 32+ A 4 x 42+ A 5 x 52= A 2.
Таблица 2.1
| А1 | A2 | A3 | А4 | А5 | а0 |
Решая эти уравнения, получим
х 31=1; x 41=0; х51=1; x 32=0; х42=1; х52=1.
3. Находим симплекс-разности для небазисных переменных x1 и x2:
с 1- с 3 х 31- с 4 х 41- с 5 х 51= с 1=2;
с 2- с 3 х 32- с 4 х 42- с 5 х 52= с 2=5.
Поскольку с 2> с 1, вводим в базис вектор x2.
4. Определяем, какая переменная выводится из базиса. Для этого находим
х 3= х 3* - х 2 х 32= х 3*;
х 4= х 4* - х 2 х 42=300-1 х 2;
х 5= х 5* - х 2 х 52=500-1 х 2;
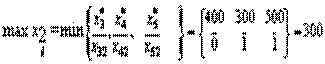
Итак переменная х 2 вводится в базис со значением x2*= 30 0, переменная x 4 выводится из базисного решения, а вектор A 4— из базиса.
Вторая итерация. 1. Раскладываем каждый из небазисных векторов через базисные { A 2, A 3, A 5}. Базисное решение
x 2*=300, х 3*=400, х 5*=500-300*1=200
Представим каждый из векторов A 1, A 4,не вошедших в базис, в виде линейной комбинации A 2, A 3, A 5.Так как вектор A 4 был выведен из базиса, рассмотрим только вектор A 1.
Уравнение будет иметь вид
A2 х 21+A3 х 31+A5 х 51=A1,
откуда х 21=0; х 31=1; х 51=1.
2. Находим симплекс-разность для переменной x 1:
с 1- с 2 х 21- с 3 х 31- с 5 х 51= с 1-0-0-0= с 1=2>0.
Итак, переменную х 1 можно ввести в базис.
3. Определяем, какую переменную (вектор) следует вывести из базиса. Для этого вычисляем
х 2= х 2* - х 1 х 21=300-0 х 1;
х 3= х 3* - х 1 х 31=400-1 х 1;
х 5= х 5* - х 1 х 51=200-1 х 1;
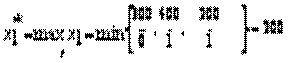
Следовательно, из базиса выводится вектор х 5 , из базисного решения – A 5.
4. Вычисляем новый ДБР.
Переходим к третьей итерации. Следующие итерации проводятся аналогично.
x 1*=200; x 2*=300.
 2015-08-21
2015-08-21 333
333







