Рассмотренный выше алгоритм симплекс-метода неудобен для программирования и решения задач на ЭВМ. Потребовалась его рационализация как по форме представления информации, так и в способе организации вычислений, чтобы сделать его пригодным для реализации на ЭВМ. С этой целью был разработан табличный вариант симплекс-метода. В его основе лежит метод полного исключения Жордана – Гаусса.
Пусть задана система линейных алгебраических уравнений
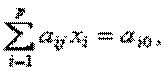 j =1, 2, …, m.
j =1, 2, …, m.
В матричной форме данная система имеет следующий вид:
Ax=A0.
Матрица A p=[ A, A 0] называется расширенной матрицей. Метод полного исключения Жордана – Гаусса состоит из конечного числа однотипных итераций и заключается в сведении матрицы к единичному виду. Метод основывается на двух операциях:
1) одну из строк расширенной матрицы умножают на множитель, отличный от нуля;
2) из каждой строки расширенной матрицы вычитают одну строку, умноженную на некоторое число.
Каждое из таких элементарных преобразований (называемых преобразованием Гаусса) приводит к новой системе линейных уравнений, которая эквивалентна начальной системе.
Первая итерация метода полного исключения.
1. Среди элементов A выбирают произвольный элемент, отличный от нуля. Его называют направляющим элементом итерации. Строку и столбец, содержащие направляющий элемент, называют направляющими.
2. Все элементы направляющей строки расширенной матрицы делят на направляющий элемент. В результате получают направляющую строку с направляющим элементом, равным единице. Далее из элементов каждой строки матрицы A вычитают элементы новой направляющей строки, умноженные на элементы, которые расположены на пересечении данной строки и направляющего столбца.
Матрицу, в которую преобразовалась расширенная матрица A p после первой итерации, обозначим A p(1). В ней все элементы направляющего столбца, кроме направляющего элемента (равного 1), стали нулями. Совокупность элементов первых n столбцов матрицы A p, лежащих вне направляющей строки и столбца предыдущей (предыдущих) итерации называют главной частью матрицы A p(1).
Вторая и дальнейшие итерации метода проводятся аналогично первой, причем до тех пор, пока имеется возможность выбора направляющего элемента.
Если после k -йитерации главная часть матрицы A p(k) не содержит ни одного элемента или содержит только нули, то процесс заканчивается.
Пусть процесс оборвался после итерации 1. Предположим вначале, что среди строк матрицы A (l) есть такие, которые не были направляющими ни в одной из предыдущих итераций, например, строка с номером i. Тогда очевидно,
aij = 0; j = 1, 2, …, n.
Поскольку для любой строки справедливо
A (i) x = ai 0 , (2.2.9)
то уравнение для і-й строки имеет вид
0 x 1+0 x 2+…+0 xn = ai 0(l). (2.2.10)
Если ai 0 (l) ≠0, то уравнение (2.2.10) противоречиво, и данная система уравнений неразрешима.
Если ai 0 (l) =0, то уравнение (2.2.10) представляет собой тождество и
i -я строка может быть отброшена.
Перебрав одну за другой все строки матрицы A (l), которые не являлись направляющими, либо устанавливают неразрешимость системы уравнений, либо отбрасывают все нулевые строки.
Таким образом, в системе окажется равно l уравнений. Примем для определенности, что это первые по порядку l уравнений. Тогда полученную систему уравнений можно записать в виде
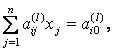 i =1, 2, …, l. (2.2.11)
i =1, 2, …, l. (2.2.11)
Пусть i -й направляющей строке соответствует i-й направляющий столбец вследствие соответствующего выбора направляющего элемента. Тогда
aij (l)= 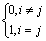 i =1, 2, …, l. (2.2.12)
i =1, 2, …, l. (2.2.12)
Следовательно, (2.2.11) можно записать в виде:
xi = ai0(l) - 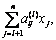 i =1, 2, …, l, (2...2.13)
i =1, 2, …, l, (2...2.13)
причем переменные xi (i =1, …, l) являются базисными, а переменные xj
(j = l +1, …, n) – небазисными.
При xj = 0 (j = l +1, …, n) получим одно из базисных решений системы уравнений
xi = ai 0(l), i =1, 2, …, l, xj =0; j = l +1,…, n.
Задавая для xj произвольные значения 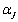 , получим полное множество решений.
, получим полное множество решений.
Если xi - i –я компонента этого решения, то
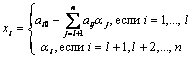 (2.2.14)
(2.2.14)
Обозначим
x 0= (a 10, a 20,…, al 0,0,…,0)
x j = (– a 1 j , –a 2 j ,…, –aij, 0,…, 0, 1, 0,…,0), 1 £ j £ n.
j n
Тогда общее (полное) решение системы линейных уравнений определяется соотношением, аналогичным (2.2.14):
x общ = x 0 + 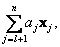 (2.2.15)
(2.2.15)
где x 0 – базисное решение начальной системы уравнений;
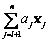 – полное решение соответствующей однородной системы уравнений (то есть при A 0=0).
– полное решение соответствующей однородной системы уравнений (то есть при A 0=0).
Обозначим расширенную матрицу системы уравнений после k- й итерации через
A p(k)=[ ai 0(k), ai 1(k),…, ain (k)], i =1,2,…, m.
Пусть aij (k)– направляющий элемент преобразования на (k + 1)-й итерации. Тогда в результате (k + 1)-й итерации метода полного исключения Гаусса получим матрицу Ap(k +1), элементы которой определяются следующими соотношениями:
1) для всех элементов направляющей строки
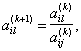 l =1, 2,…,n; (2...2.16)
l =1, 2,…,n; (2...2.16)
2) для элементов направляющего столбца
arj (k+ 1) =0; r =1,…, n, причем r ¹ и; aij (k+ 1)=1; (2.2.17)
3) для всех остальных элементов матрицы
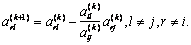 (2.2.18)
(2.2.18)
Пример 2.3. Применим метод полного исключения Гаусса для исследования системы уравнений
x1 + 2 x2 + x3 + x4 = 3;
2 x1 + x2 + x3 + 3 x4 = 3;
4 x1 + 5 x2 + 3 x3 + 5 x4 = 9.
Расширенная матрица имеет вид:

Первая итерация. В качестве первого направляющего элемента возьмем a11= 1, умножим первую строку матрицы А на 2 и на 4, затем вычитая результаты из второй и третьей строк, получим

Вторая итерация. Поскольку главная часть матрицы A p(1) содержит ненулевые элементы, продолжим процесс исключения. Выберем элемент a22(1)=-3.
После аналогичных преобразований получим

Как видим, главная часть матрицы A p(2), состоящая из элементов a33(2) и a34(2), содержит только нули. Следовательно, процесс исключения заканчивается.
Исследуем матрицу A (2). Поскольку третья строка содержит лишь нулевые элементы, то она может быть отброшена. Тогда эквивалентная матрица системы уравнений будет иметь вид

Соответственно формулам (2.2.13), (2.2.14) имеем базисное решение
x1*=1; x2*=1; x3=0; x4=0.
Общее решение данной системы имеет такой вид:
X1=1- 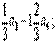 X2=1-
X2=1- 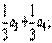 X3 =
X3 = 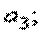 X4=
X4= 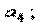
где a 3, a 4– произвольные скаляры.
 2015-08-21
2015-08-21 562
562








