Симплекс-метод

Для 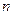переменных областью допустимых решений является многомерный многогранник, подобный симплексу. Оптимальное решение, как правило, это вершина (граничная точка) такого многогранника. Симплекс-метод заключается в последовательном целенаправленном обходе вершин симплекса. В каждой следующей граничной точке симплекса значение целевой функции, в общем случае, улучшается. Для применения симплекс-метода ЗЛП следует записать в канонической форме:

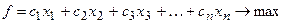
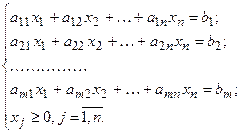
В канонической форме все переменные неотрицательны, ограничениями являются уравнения, и требуется найти такие значения 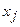, , 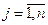при которых целевая функция имеет максимум.

ОЗЛП не всегда имеет решение: уравнения могут оказаться несовместными; уравнения могут оказаться совместными, но не в области неотрицательных решений; допустимые решения существуют, но среди них нет оптимального: целевая функция не ограничена в области допустимых решений.

Симплекс-метод является методом направленного перебора решений системы. Каждое следующее решение улучшает значение целевой функции.

· Определение начального решения, удовлетворяющего ограничениям ОЗЛП

· Последовательное улучшение начального решения и получение оптимального решения задачи.