2) Решим симплекс-методом задачу с искусственным базисом (хотя бы один знак неравенств-ограничений " ≥ " или " = ").
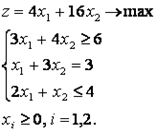
Запишем задачу в канонической форме (в виде системы уравнений, что требует симплекс-метод), для этого введем две переменные х3 ≥ 0 и х4 ≥ 0 получим:
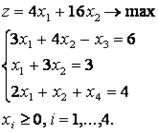
Система ограничений предлагает только одну допустимую базисную переменную x4, только она входит только в одно уравнение в третье с коэффициентом 1, поэтому в первое и второе уравнения добавляем искусственные переменные R1 ≥ 0 и R2 ≥ 0 Чтобы можно было применить симплекс-метод система уравнений-ограничений должна быть системой с базисом, т.е. в каждом уравнении должна быть переменная с коэффициентом 1, которая входит только в одно уравнение системы, в нашем случае это R1, R2 и x4. Получили, так называемую, М-задачу:
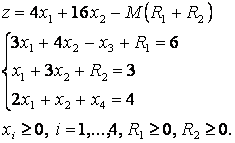
Данная система является системой с базисом, в которой R1, R2 и x4 базисные переменные, а x1, x2 и x3 свободные переменные, свободные члены всех уравнений неотрицательны. Следовательно, для решения задачи можно применить симплекс-метод. Запишем начальную симплекс-таблицу:
симплекс-метод итерация 0
| БП | x1 | x2 | x3 | R1 | R2 | x4 | Решение | Отношение |
| z | -4 | -16 | - | |||||
| R1 | -1 | 6/4=3/2 | ||||||
| R2 | 3/3=1 | |||||||
| x4 | 4/1=4 | |||||||
| Оценка | -4 | -7 | -1 | -1 | - | - |
В таблицу для задач с искусственным базисом добавлена строка «Оценка». Она получается суммированием соответствующих коэффициентов строк с искусственными переменными (R) с обратным знаком. Она будет присутствовать в таблице до тех пор, пока хотя бы одна из искусственных переменных есть в базисе. По наибольшему по модулю отрицательному коэффициенту строки "Оценка" определяется разрешающий столбец пока она есть в таблице. Когда строка "Оценка" выйдет из таблицы (в базисе нет искусственных переменных) разрешающий столбец будет определяться по z-строке, как и в задаче с начальным базисом. В данной таблице разрешающий столбец х2, он выбран по наибольшей по модулю отрицательной оценке (-7). Разрешающая строка R2 выбрана по наименьшему отношению столбца "Решение" к соответствующим положительным элементам разрешающего столбца, как и в задаче без искусственных переменных. Это значит, что на следующей итерации симплекс-метода переменная х2 из свободной перейдет в базисную, а переменная R2 из базисной – в свободную. Запишем следующую симплекс-таблицу:
симплекс-метод итерация 1
| БП | x1 | x2 | x3 | R1 | R2 | x4 | Решение | Отношение |
| z | 4/3 | 16/30 | - | |||||
| R1 | 5/3 | -1 | -4/3 | 6/5 | ||||
| x2 | 1/3 | 1/3 | ||||||
| x4 | 5/3 | -1/3 | 9/5 | |||||
| Оценка | -5/3 | -1 | 4/3 | - | - |
Разрешающий столбец х1, разрешающая строка R1, R1 выходит из базиса, x1 входит в базис. После этого в базисе не остается искусственных переменных, поэтому строки «Оценка» в следующей таблице нет:
симплекс-метод итерация 2
| БП | x1 | x2 | x3 | R1 | R2 | x4 | Решение | Отношение |
| z | 4/5 | -4/5 | 32/5 | 72/5 | - | |||
| x1 | -3/5 | 3/5 | -4/5 | 6/5 | - | |||
| x2 | 1/5 | -1/5 | 3/5 | 3/5 | - | |||
| x4 | -1 | - |
Далее разрешающий столбец выбирается по z-строке. В z-строке все коэффициенты неотрицательны кроме коэффициента при искусственной переменной R1, который не влияет на оптимальность, когда искусственные переменные вышли из базиса. Следовательно, симплекс-методом получено оптимальное решение x1 = 6/5; x2 = 3/5; zmax = 72/5.
 2015-08-21
2015-08-21 383
383








