Составляющие и формы систем уравнений в эконометрических исследованиях

При рассмотрении систем одновременных уравнений перемен­ные делятся на два больших класса — эндогенные и экзогенные пере­менные. Эндогенные переменные — это переменные, значение которых определяются внутри модели и обозначаются обычно как у. Экзогенные переменные — это внешние по отношению к модели переменные, их значения определяются вне модели и поэтому они считаются фикси­рованными, обозначаются обычно как х.

Различают несколько видов систем уравнений, применяемых в экономет­рике:

1. С истема независимых уравнений - когда каждая зависимая переменная 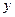рассматривается как функция одного и того же набора факторов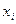

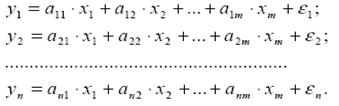
Набор факторов 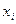в каждом уравнении может варьировать. Отсут­ствие того или иного фактора в уравнении системы может быть след­ствием как экономической нецелесообразности его включения в мо­дель, так и несущественности его воздействия на результативный при­знак.

Каждое уравнение системы независимых уравнений может рассмат­риваться самостоятельно. Для нахождения его параметров использует­ся метод наименьших квадратов.

2. Система рекурсивных уравнений, когда зависимая переменная у включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений на­ряду с набором собственно факторов х.

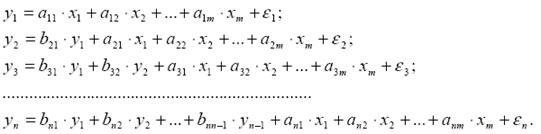
В таких моделях уравнения оцениваются поэтапно 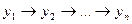. Модели данного типа встречают­ся достаточно редко.

3. Система взаимозависимых, совместных, одновременных, уравне­ний (или структурная форма модели) в ней одни и те же зависи­мые переменные в одних уравнениях входят в левую часть, а в других уравнениях — в правую часть системы.

В данной системе одни и те же переменные одновременно рас­сматриваются как зависимые в одних уравнениях и как независимые в других. Системы совместных уравнений получили наибольшее рас­пространение в эконометрических исследованиях

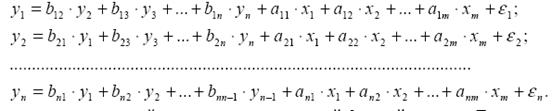
Рассмотрим в качестве примера эконометрическую модель страны:

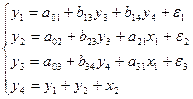
где 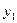- расходы на конечное потребление данного года, 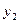- валовые инвестиции в текущем году, 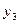- расходы на заработную плату в текущем году, 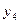- валовой доход за текущий год, 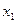- валовой доход предыдущего года, 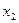- государственные расходы текущего года, 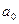- свободный член уравнения, 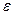- случайные ошибки.

Система «объясняет», а также прогнозирует столько результативных признаков, сколько уравнений входит в систему. Системы могут состоять из тождеств (четвертое уравнение) и регрессионных (поведенческих) уравнений (первые три), каждое из которых может, кроме объясняющих переменных, включать в себя также объясняемые переменные из других уравнений системы. Таким образом, имеется набор объясняемых переменных, связанных через уравнения системы. Для тождеств характерно, что их вид и значения параметров известны. В поведенческих уравнениях значения параметров требуется оценить. В приведенном выше примере переменные 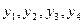определяются из уравнений модели, т.е. являются объясняемыми переменными, а переменные 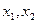- объясняющие переменные. Разделение ролей между переменными в системе одновременных уравнений может быть проинтерпретировано следующим образом: переменные 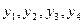формируют свои значения внутри модели. Такие переменные называются эндогенными. Переменные 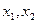считаются в уравнениях заданными, их значения формируются вне модели. Такие переменные называются экзогенными.