Двухшаговый метод наименьших квадратов (ДМНК)

Оценка сверхидентифицированного уравнения осуще­ствляется при помощи двухшагового метода наименьших квадратов.

Алгоритм ДМНК включает следующие шаги:

1) составление приведенной формы модели;

2) применение обычного МНК к каждому уравнению приведенной формы и получение численных оценок приве­денных параметров;

3) определение расчетных значений эндогенных пере­менных, которые фигурируют в качестве факторов в струк­турной форме модели;

4) определение структурных параметров каждого уравнения в отдельности обычным МНК, используя в каче­стве факторов входящие в это уравнение предопределенные переменные и расчетные значения эндогенных переменных, полученные на шаге 1.

Основная идея ДМНК — на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения.

Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Метод получил название двухшагового МНК, ибо дважды используется МНК: на первом шаге при определении

приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной 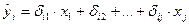и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических

(расчетных) значений эндогенных переменных.

Сверхидентифицируемая структурная модель может быть двух типов:

• все уравнения системы сверхидентифицируемы;

• система содержит наряду со сверхидентифицируемыми точно

идентифицируемые уравнения.

Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения исполняется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.

ДМНК является наиболее общим и широко распространенным методом решения системы одновременных уравнений. Для точно идентифицируемых уравнений ДМНК дает тот же результат, что и КМНК.

Несмотря на важность системы эконометрических уравнений, на практике часто не принимают во внимание некоторые взаимосвязи, применение традиционного МНК к одному или нескольким уравнениям также широко распространено в эконометрике.

В частности, при построении производственных функций анализ спроса можно вести, используя обычный МНК.

Пример

Изучается модель вида

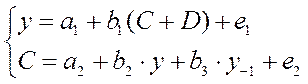
где у - валовой национальный доход;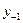

- валовой национальный доход предшествующего года;

С - личное потребление;

D - конечный спрос (помимо личного потребления);

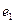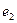, - случайные составляющие.

Информация за девять лет о приростах всех показателей дана в табл.1

Таблица 1

Год	D		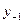y	C
	-6,8	46,7	3,1	7,4
	22,4	3,1	22,8	30,4
	-17,3	22,8	7,8	1,3
	12,0	7,8	21,4	8,7
	5,9	21,4	17,8	25,8
	44,7	17,8	37,2	8,6
	23,1	37,2	35,7	30,0
	51,2	35,7	46,6	31,4
	32,3	46,6	56,0	39,1
Сумма	167,5	239,1	248,4	182,7

Для данной модели была получена система приведенных урав­нений:

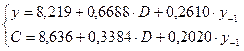
Требуется:

1. Провести идентификацию модели.

2. Рассчитать параметры первого уравнения структурной модели.

Решение

1. В данной модели две эндогенные переменные (у и С) и две экзо­генные переменные (D и 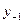). Второе уравнение точно идентифици­ровано, так как содержит две эндогенные

переменные и не содержит одну экзогенную переменную из системы. Иными словами, для вто­рого уравнения имеем по счетному правилу идентификации равен­ство: 2=1 + 1.

Первое уравнение сверхидентифицировано, так как в нем на па­раметры при С и D наложено ограничение: они должны быть равны. В этом уравнении содержится одна эндогенная переменная у. Пере­менная С в данном уравнении не рассматривается как эндогенная, так как она участвует в уравнении не самостоятельно, а вместе с пе­ременной D. В данном уравнении отсутствует одна экзогенная пере­менная, имеющаяся в системе. По счетному правилу идентификации получаем: 1 + 1 = 2: D + 1 > Н. Это больше, чем число эндогенных переменных в данном уравнении, следовательно, система сверх-идентифицирована.

2. Для определения параметров сверхидентифицированной модели используется двухшаговый метод наименьших квадратов.

Шаг 1. На основе системы приведенных уравнений по точно идентифицированному второму уравнению определим теоретиче­ские значения эндогенной переменной С. Для этого в приведенное уравнение

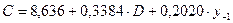
подставим значения D и 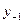, имеющиеся в условии задачи. Получим:

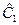= 15,8; 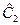= 16,8; 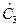= 7,4; 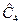= 14,3; 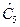= 15,0; 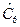= 27,4; 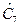= 24,0;

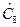= 33,2; 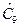= 29,0.

Шаг 2. По сверхидентифицированному уравнению структурной формы модели заменяем фактические значения С на теоретические 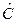и рассчитываем новую переменную 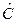+ D (табл. 2).

Таблица 2

Год	D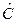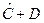
	-6,8	15,8	9,0
	22,4	16,8	39,2
	-17,3	7,4	-9,9
	12,0	14,3	26,3
	5,9	15,0	20,9
	44,7	27,4	72,1
	23,1	24,0	47,1
	51,2	33,2	84,4
	32,3	29,0	61,3
Сумма	167,5	182,7	350,2

Далее к сверхидентифицированному уравнению применяется метод наименьших квадратов. Обозначим новую переменную 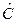+ D через Z. Решаем уравнение

.

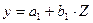Система нормальных уравнений составит:

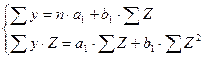
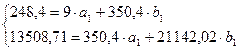
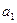= 7,678; 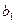= 0,512.

Итак, первое уравнение структурной модели будет таким:

у=7,678 + 0,512 (С + D).

Поскольку второе уравнение точно идентифицировано, то оценка его параметров может быть дана с помощью косвенного метода наименьших квадратов (КМНК).

Исходя из приведенной модели, выразим переменную D из первого уравнения системы и подставим во второе уравнение:

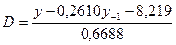
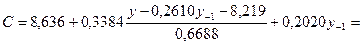
=8,636+0,506y-0,1321 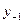-4,1587+0,2020 =

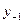=4,4773+0,506y+0,699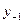

Это же уравнение C=4,4773+0,506y+0,699 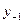можно получить, применяя ДМНК ко второму структурному уравнению. В этом случае сначала определяем 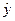из первого уравнения приведенной системы, подставляя в него значения D и 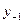, а затем используем МНК к уравнению .

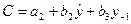При этом 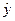составит:

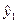=15,86; 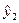=24,01; 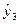=2,60; 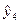=18,28; 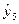=17,75;

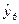=42,76; 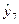=33,38; 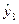=51,78; 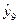=41,98; 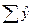=248,4

что указывает на правильность расчетов, ибо 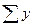= =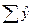248,4.

Применяя МНК по второму структурному уравнению и используя при этом не фактические значения y, а расчетные, т.е. 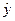, получим систему нормальных уравнений:

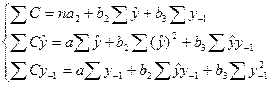
По данным примера получаем:

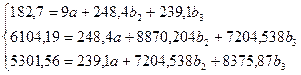
Откуда

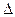=33391334; 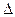a=149485264;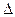 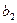=16896029;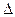 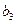=2334321;

a=4,4768; 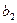=0,506; 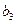=0,699

Соответственно второе структурное уравнение составит:

y=4, 4768+0,506y+0,699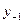

Как видим, результат совпадает с КМНК, но трудоемкость вычислений возросла.