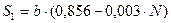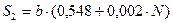2015-09-07
300
,
,
точка 2 слева от линии AB.
Расстояние b взять из решения Рисунок 6
обратной задачи (таблица 1).
Относительную ошибку измерения расстояний принять равной
.
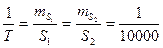Графическое решение:
- провести окружность с центром в пункте A радиусом S1;
- провести окружность с центром в пункте B радиусом S2;
- точка пересечения окружностей является искомой точкой 2; задача имеет два решения, поэтому из двух точек пересечения окружностей нужно выбрать ту, которая находится справа (слева) от линии AB в соответствии с номером варианта.
Аналитическое решение:
- в треугольнике AB2 по теореме косинусов вычислить углы β1 и β2
,
;
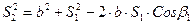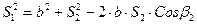- вычислить угол γ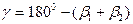 
;
- вычислить дирекционные углы сторон A2 и B2:
точка 2 справа от линии AB
,
;
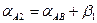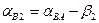точка 2 слева от линии AB
,
;
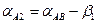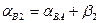дирекционный угол αAB следует взять равным углу α из решения обратной геодезической задачи (таблица 1);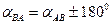 
;
- решить прямые геодезические задачи:
из пункта A на точку 2
,
,
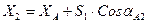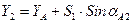и из пункта B на точку 2
,
;
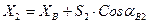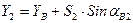расхождение координат X2 и Y2 по двум решениям не должно превышать 0,02 м;
- вычислить ошибку положения точки 2 по формуле
.
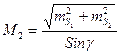Пример решения линейной засечки приведён в таблице 4.
Напоминание: При выполнении операций 19 и 20 искомый угол (β1 или β2) следует перевести из десятичной формы в полную форму, округлить до целых секунд и затем уже записать в таблицу вычислений. Перед выполнением операций 23 и 24 нужно перевести в десятичную форму угол αA2; перед выполнением операций 25 и 26 нужно перевести в десятичную форму угол αB2.
Таблица 4 - Решение линейной засечки
| № п/п | Обозначения (вариант чётный) | Вычисления |
| b (м) S1 S2 (справа) b2 S12 S22 | 1 499, 78 1 000, 00 1 200, 00 2 249 340 1 000 000 1 440 000 | |
b2 + S12 − S22
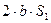Cos β1 = (13) / (14)
| 1 809 340 2 999 560 + 0, 603 202 | |
| αAB β1 = arcos (15) αA2 = (6) + (19) | 3040 07’ 08” 52 54 02 357 01 10 | |
XA (м)
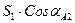X2 = (1) + (23)
Y2 = (2) + (24)
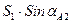YA
| 6 643 000, 00 + 998, 65 6 642 998, 65 7 374 948, 00 − 52, 00 7 375 000, 00 | |
b2 + S22 − S12
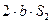Cos β2 = (16) / (17)
| 2 689 340 3 599 472 + 0, 747 148 | |
| αBA = αAB ± 1800 β2 = arcos (18) αB2 = (7) − (20) | 1240 07’ 08” 41 39 22 82 27 46 | |
XB (м)
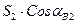X2 = (3) + (25)
Y2 = (4) + (26)
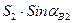YB
| 6 642 841, 24 + 157, 40 6 642 998, 64 7 374 948, 00 + 1 189, 63 7 373 758, 37 | |
| γ | 850 26’ 36” | |
| M2 (м) | 0, 16 |
