Формула линзы

Связь между фокусным расстоянием линзы, расположением предмета перед линзой и расстоянием от линзы до изображения можно вычислить не прибегая к геометрическим построениям. Это можно сделать с помощью формулы линзы.

Для тонких симметричных линз эта формула имеет вид:

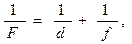(5.3)

где 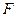- фокусное расстояние, м;

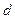- расстояние от предмета до линзы, м;

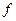- расстояние от линзы до изображения, м.

Величина 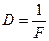называется оптической силой линзы и измеряется в диоптриях (1 Дп = 1 м^-1)

Принятые обозначения проиллюстрированы на рис.12.

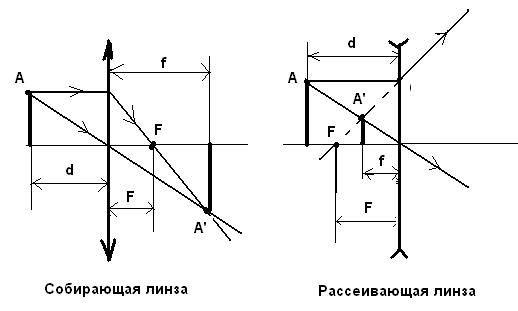
Рис.12

Важно отметить, что величины 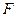и 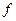отсчитываются от оси линзы в сторону хода луча и, следовательно, положительны за линзой и отрицательны перед ней. Это значит, что для собирающей линзы всегда 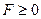, а для рассеивающей 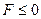. Кроме того, если в результате расчета окажется 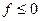, то это означает, что изображение находится перед линзой и является мнимым.

Величина 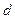отсчитывается от предмета до линзы и всегда положительна.

Проанализируем теперь свойства линз с помощью уравнения линзы. Из (5.3) нетрудно получить уравнение для нахождения расстояния от линзы до изображения:

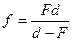, (5.4)

а также коэффициент увеличения 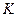, т.е отношение размера изображения к размеру предмета (очевидно, что / )

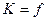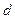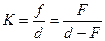(5.5)

Для рассеивающей линзы 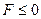из (5.4)и (5.5) следует, что 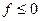и 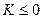, т.к. числитель в этих формулах отрицателен, а знаменатель положителен. Это соответствует мнимому изображению. Кроме того, очевидно 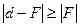и следовательно 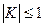, т.е изображение уменьшенное.

Таким образом, в рассеивающей линзе изображение всегда мнимое и уменьшенное.

Для собирающей линзы 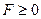и из (5.4) и (5.5) следует, что:

1. При 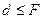величины 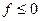и 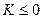, т.е. изображение мнимое. Поскольку 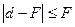, то 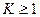, т.е изображение увеличенное

Таким образом, если предмет находится между передним фокусом и линзой, то его изображение мнимое и увеличенное.

2. При 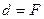из (5.4) и (5.5) формально следует, что изображение находится на бесконечном удалении от линзы. На самом деле изображение в линзе отсутствует, т.к. проходящие через линзу лучи параллельны.

3. При 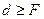величины 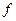и 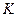положительны, т.е. изображение действительное, причем

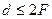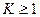- если , то и изображение увеличенное;

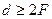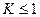- если , то и изображение уменьшенное.

Уравнение линзы не дает ответ на вопрос о расположении (прямое или перевернутое) изображения. Отметим, что в случае 1 изображение прямое, а в случаях 2 и 3 - перевернутое. Убедитесь в правильности последнего утверждения сами, построив изображение спички в собирающей линзе.