1. Областью значений функции 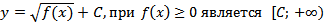 .
.
2. Число точек разрыва и число вертикальных асмптот функции 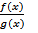 равно числу корней знаменателя g(x)= 0.
равно числу корней знаменателя g(x)= 0.
3. 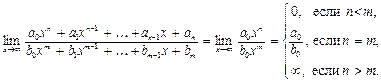
4. Первый замечательный предел 
5. Второй замечательный предел 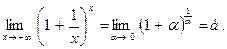
Пример: 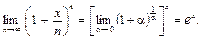
6. Таблица производных основных элементарных функций.
1) 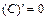 , C – постоянное число; 6)
, C – постоянное число; 6) 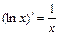 ;
;
2) 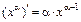 , 7)
, 7) 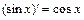 ;
;
α– действительное число; 8) 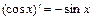 ;
;
α = 1: 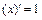 ; 9)
; 9) 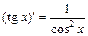 ;
;
α = 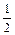 :
: 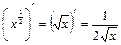 ; 10)
; 10) 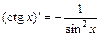 ;
;
α 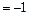 :
: 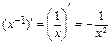 ; 11)
; 11) 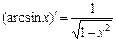 ;
;
3) 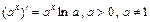 ; 12)
; 12) 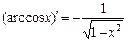 ;
;
4) 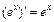 ; 13)
; 13) 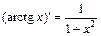 ;
;
5) 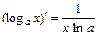 ; 14)
; 14) 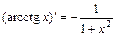 .
.
7. Правила дифференцирования.
1) 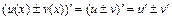 ;
;
2) 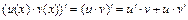 ;
;
3) 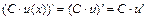 ; C – постоянное число;
; C – постоянное число;
4) 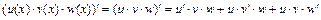 ;
;
5) 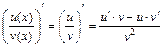 .
.
6) Т е о р е м а. Пусть y = f (u), где u = φ(x). Тогда производная сложной функции y = f [φ(x)] находится по правилу:
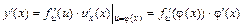 ,
,
где нижний индекс указывает, по какой переменной находится производная.
8. Частныепроизводные 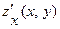 и
и 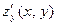 функции двух переменных z = f (x, y) находятся по этим же формулам и правилам: при нахождении
функции двух переменных z = f (x, y) находятся по этим же формулам и правилам: при нахождении 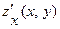 считается постоянным число y; при нахождении
считается постоянным число y; при нахождении 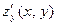 постоянным числом считается x.
постоянным числом считается x.
9. Наклонная асимптота функции 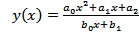 имеет уравнение
имеет уравнение 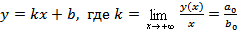 . Далее уравнение асимптоты смотри в ответе по значению k.
. Далее уравнение асимптоты смотри в ответе по значению k.
10. Таблица интегралов.
1) 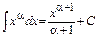 , α ≠ –1; α = 0:
, α ≠ –1; α = 0: 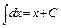 ;
;
α = 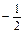 :
: 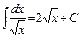 ; α =
; α = 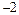 :
: 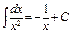 .
.
2) 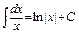 . 3)
. 3) 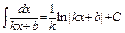 .
.
4) 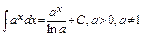 . 5)
. 5) 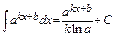 .
.
6) 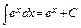 . 7)
. 7) 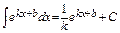 .
.
8) 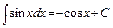 . 9)
. 9) 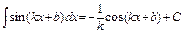 .
.
10) 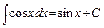 . 11)
. 11) 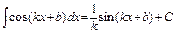 .
.
12) 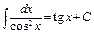 . 13)
. 13) 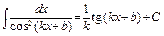 .
.
14) 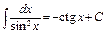 . 15)
. 15) 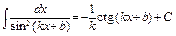 .
.
16) 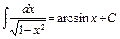 . 17)
. 17) 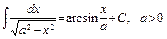 .
.
18) 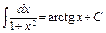 . 19)
. 19) 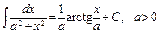 .
.
20) 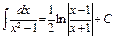 . 21)
. 21) 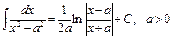 .
.
22) 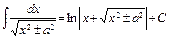 .
.
7. Формула замены переменной в неопределенном интеграле.
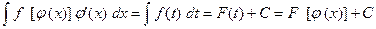 .
.
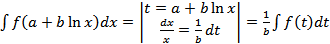 .
.
8. Формула интегрирования по частям.
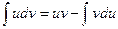 .
.
9. Формула Ньютона – Лейбница.
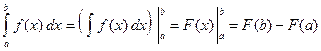 .
.
10. Основные свойства определенного интеграла.
1) 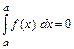 ; 2)
; 2) 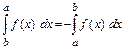 ;
;
3) 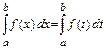 ; 4)
; 4) 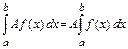 , A ≠0 – постоянная;
, A ≠0 – постоянная;
5) 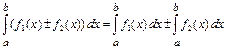 ;
;
6) если a < c < b, то 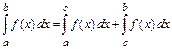 .
.
Например: 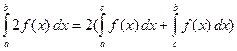 .
.
11. Площадь фигуры, ограниченной линиями x = a, x = b, y=f1(x), y=f2(x), где f1(x)≤ f2(x):
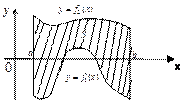 |
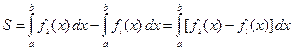 .
.
 2015-09-07
2015-09-07 225
225








