Аналитическая геометрия
1. Расстояние между двумя точками M1 (x1,y1) и M2 (x2,y2) равно:
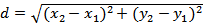 .
.
2. Уравнения прямой: Ax+By+C=0 – общее; 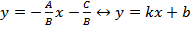 – уравнение с угловым коэффициентом k=tg α, где α – угол наклона прямой к оси Ох.
– уравнение с угловым коэффициентом k=tg α, где α – угол наклона прямой к оси Ох.
3. Условия параллельности и перпендикулярности прямых y=k1x+b1 и y=k2x+b2: параллельны, если k2=k1; перпендикулярны, если k2k1= - 1.
4. Кривые второго порядка: 1) (x-a)2+(y-b)2=R2 – уравнение окружности радиуса R с центром в точке C(a,b); 2) 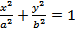 - уравнение эллипса, где
- уравнение эллипса, где 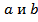 - полуоси;
- полуоси;
3) 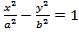 - уравнение гиперболы,
- уравнение гиперболы, 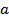 - действительная полуось,
- действительная полуось, 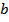 - мнимая полуось;
- мнимая полуось;
4) 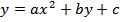 - уравнение параболы.
- уравнение параболы.
5. Уравнение плоскости: A x+ B y+ C z+ D =0, где 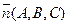 - нормальный вектор.
- нормальный вектор.
Линейная алгебра
1. Вычисление определителей: 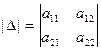
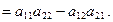
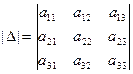
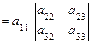
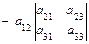
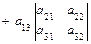 .
.
Правило Сарруса:

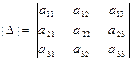
2. Линейные операции над матрицами:
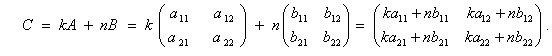
3. Умножение матриц:
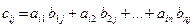
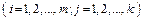
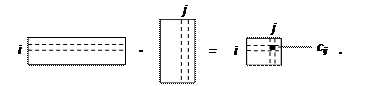 |
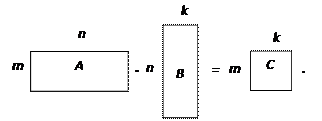
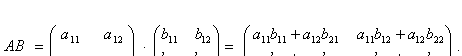
4.
 |
Матрица АТ называется транспонированной матрицей А, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы АТ. При транспонировании меняется строение матрицы: если А имеет размеры m × n, то АТ имеет размеры n×m.
|
|
|
5. Если 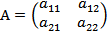 , то обратная матрица
, то обратная матрица 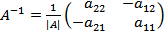 , где
, где
|A| - определитель.
6. Квадратная матрица А называется невырожденной, если ее определитель отличен от нуля |A|≠0. При |A|=0 матрица А называется вырожденной. Для существования обратной матрицы 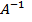 необходимо и достаточно, чтобы |A|≠0.
необходимо и достаточно, чтобы |A|≠0.
7. Алгеброическим дополнением A ij элемента aij матрицы А порядка n называется число
A ij = (-1) i+j M ij, где M ij – определитель (минор) матрицы (n-1)-го порядка, получаемый из |A| вычеркиванием i -й строки и j -го столбца.
8. Решение линейной системы ∑ aij xj = bi по формулам Крамера 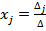 существует, если определитель системы D, составленный из коэффициентов aij, отличен от нуля D≠0.
существует, если определитель системы D, составленный из коэффициентов aij, отличен от нуля D≠0.
9. В системе m независимых уравнений с n переменными число свободных переменных равно n-m.
10.  Ранг матрицы r(A) равен числу единиц на главной диагонали при обнуливании элементов ниже диагонали методом Жордана-Гаусса.
Ранг матрицы r(A) равен числу единиц на главной диагонали при обнуливании элементов ниже диагонали методом Жордана-Гаусса.
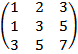
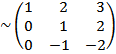
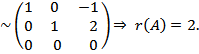
11. Собственным значением λ матрицы А называется корень квадратного уравнения, заданного определителем 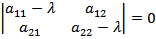 .
.
12. Квадратичной формой матрицы 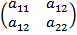 назывется трехчлен
назывется трехчлен 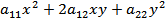 .
.
 2015-09-07
2015-09-07 331
331







