Этот метод является более точным при установлении линейной корреляции между y и x j, так как он основан не на визуальном восприятии графического представления случайных чисел, а на математических расчетах и постулатах.
Рассмотрим самый простой случай: корреляцию между двумя случайными величинами (y и х).
Присвоим каждой точке на поле корреляции свой номер i (такой же номер будет и у взаимосвязанной пары координат этой точки). Обозначим N общее число точек с координатами y i и x i. Тогда выборочный коэффициент парной корреляции можно рассчитать по формуле
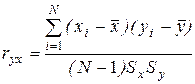 ,
,
где` y - общее среднее арифметическое значение y; ` x - общее среднее арифметическое значение х; S x и S y - выборочные абсолютные стандартные отклонения соответственно х и y (эти параметры используются как характеристики рассеивания единичных значений х и y относительно их общих средних арифметических значений).
Общие средние арифметические значения находят по формулам
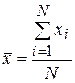 ;
; 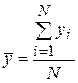 .
.
Выборочные абсолютные стандартные отклонения х и y можно рассчитать следующим образом:
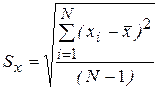 ;
; 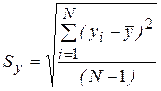 .
.
Выборочный коэффициент парной корреляции имеет следующие свойства:
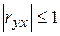 .
.
Величина r yx не изменяется при изменении начала отсчета величин, а также масштаба координатных осей y и х.
В величине r yx одновременно заложена доля случайности и нелинейности связи между y и х.
По величине и знаку r yx можно сделать большинство выводов корреляционного анализа (табл. 6). Однако выводы корреляционного анализа можно делать только после доказательств равенства или отличия от нуля рассчитанного значения r yx методами математической статистики (так называемая статистическая проверка нуль-гипотезы). С методами проверки нуль-гипотезы r yx познакомьтесь самостоятельно в [6,8].
Как следует из табл. 6, значение r yx позволяет сделать все выводы только в случае линейной зависимости y от х. При нелинейных зависимостях y от х значение r yx однозначно определяет только их знак, а для формулировки остальных выводов нужно анализировать и поле корреляции. Совместный анализ r yx и поля корреляции необходим в случае, когда r yx = 0 (r yx является "незначимым").
Более сложные случаи корреляционного анализа возникают при влиянии на случайную величину (y) нескольких случайных величин (х 1, х 2,... x j). В такой ситуации анализируют выборочные коэффициенты частной и множественной корреляции. Анализ частных и множественных коэффициентов корреляции позволяет разобраться в ситуации, когда один из факторов не оказывает непосредственного влияния на y, хотя их парный коэффициент корреляции отличен от нуля.
Более подробно с особенностями проведения корреляционного анализа познакомьтесь самостоятельно в [6,8].
Таблица 6
Выводы корреляционного анализа в зависимости от значения r yx
| Выводы корреляционного анализа | Значения ryx |
| Наличие зависимости между y j и x z: есть |
0< 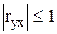 или
r yx = 0 (при наличии доказательств анализом поля корреляции); или
r yx = 0 (при наличии доказательств анализом поля корреляции);
|
| нет | r yx = 0 (при наличии доказательств анализом поля корреляции) |
| Характер и тип зависимости: "функциональная линейная" |
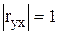
|
| "корреляционная линейная" | 0< 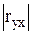 < 1 < 1
|
| Знак связи: "положительный" | r yx >0 |
| "отрицательный" | r yx <0 |
| Теснота (сила) линейной корреляционной связи | Определяется близостью к единице модуля r yx и величиной N по усмотрению исследователя |
 2015-09-06
2015-09-06 653
653








