Решение типовой контрольной работы

Задача 1. Вычислить криволинейные интегралы:

а). 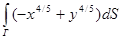, где Г – дуга кривой x^2/5+y^2/5=1, находящаяся во второй четверти.

Для параметризации кривой x^2/5+y^2/5=1 воспользуемся обобщенными полярными координатами: 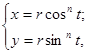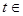[0;2π]. Если n =5, то уравнение кривой в таких координатах имеет вид: r =1. Поскольку нас интересует часть кривой, лежащая во второй четверти, то 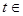[ π/2;π]. Таким образом, параметризацию кривой x^2/5+y^2/5=1 можно задать следующим образом: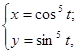 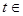[ π/2;π].

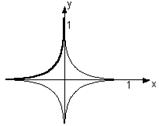рис. 8

= =

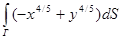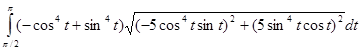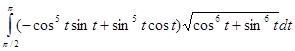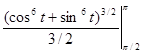=–5 =-5 = 0

б). 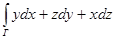, Г – линия пересечения x ²+ y ²+4 z ²=4, x= z, пробегаемая против хода часовой стрелки, если смотреть с положительной полуоси Ox.

Параметризуем кривую, она является линией пересечения эллипсоида x ²+ y ²+4 z ²=4 и плоскости x= z перпендикулярной плоскости xOz:

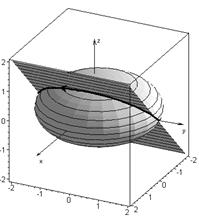рис. 9

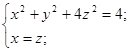
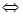
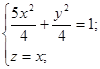
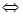
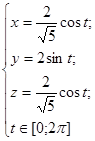
Теперь необходимо учесть ориентацию кривой, задать изменение параметра t так, чтобы пробегать кривую против хода часовой стрелки, если смотреть с положительной полуоси Ox. См. рис. 9 При такой ориентации, эллипс 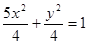, являющийся проекцией нашей кривой на плоскость xOy, также пробегаем против часовой стрелки:

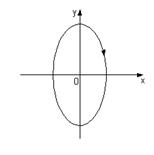рис. 10

Значит параметр t изменяется от 2π до 0.

=

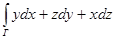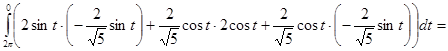
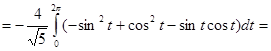
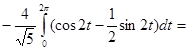
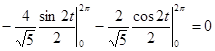
2. Применяя формулу Грина, вычислить криволинейный интеграл по замкнутой кривой Г, пробегаемой так, что ее внутренность остается слева:

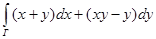, Г – окружность x²+y²=2x+4y.

Кривая Г, это окружность, с центром в точке (1;2), радиуса 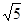, действительно, выделяя в уравнении x²+y²=2x+4y полный квадрат для x и y получаем уравнение такой окружности: (x-1)²+(y-2)²=5. Функции P (x, y)= x + y и Q (x, y)= xy - y непрерывны, вместе со своими частными производными во всех точках множества (x-1)²+(y-2)²≤5.

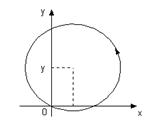рис.11

Окружность пробегаема так, что ее внутренность остается слева, значит для вычисления данного интеграла 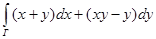можно применить формулу Грина:

= = =

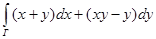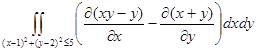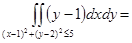
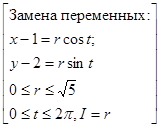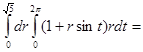
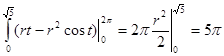
3. Вычислить поверхностные интегралы:

а). 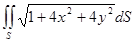, S – часть параболоида z = x ²+ y ², лежащая внутри цилиндра x²+ y ²=2x+2y.

Так как поверхность S задана в виде графика функции z = x ²+ y ², то элемент площади

dS = 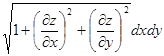= 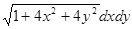, параметры x и y изменяются на множестве D ={(x, y): x ²+ y ²≤2 x +2 y }. Так как x ²+ y ²≤2 x +2 y можно преобразовать к виду (x -1)²+(y -1)²≤2, то D представляет собой круг радиуса 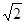, с центром в точке (1;1).

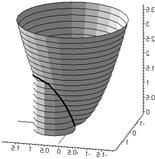рис.12

= = =

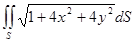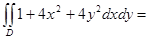
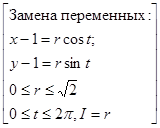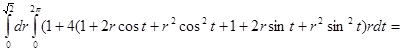
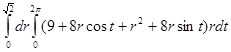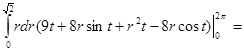
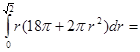
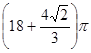
б). 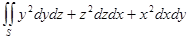, S – внешняя сторона части боковой поверхности конуса (x ²+ y ²)^1/2≤ z ≤2, x ≥0, y ≤0.

Параметризуем поверхность конуса, используя цилиндрические координаты:

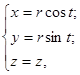0≤ t ≤2π; 0≤ r <+∞; -∞< z <+∞

В этих координатах уравнение конуса z =(x ²+ y ²)^1/2 принимает вид: z = r. Таким образом,

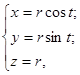0≤ t ≤2π; 0≤ r <+∞ - параметрическое задание боковой поверхности конуса z =(x ²+ y ²)^1/2. Так как x ≥0, y ≤0, то значения угла t лежат в четвертой четверти 3π/2≤ t ≤2π. Так как z ≤2, то 0≤ r ≤2. Теперь определимся с ориентацией поверхности. Найдем вектор нормали 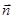= = 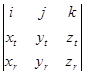= 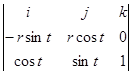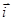r cos t + 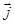r sin t - 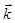r

Векторы u =(x_t, y_t, z_t), v =(x_r, y_r, z_r) в каждой точке поверхности конуса задают площадку, касательную к поверхности, ориентированную следующим образом:

рис. 13

Так как { u, v, n } должны образовывать левую тройку, то 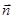– внешний вектор нормали. Следовательно:

= =

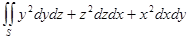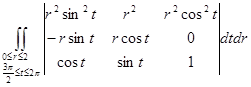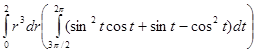=4 =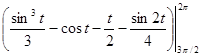

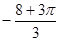
4. С помощью теоремы Гаусса-Остроградского вычислить интеграл:

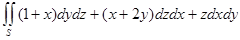, где S – внешняя сторона полной поверхности x ²+ y ²≤ z ≤4.

Заданная поверхность ограничивает множество G ={(x; y; z): x ²+ y ²≤ z ≤4}. Функции P (x; y; z)=1+ x; Q (x; y; z)= x+2y; R (x; y; z)=z непрерывны, вместе со своими частными производными в 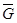. Поэтому для вычисления интеграла может быть использована формула Гаусса-Остроградского:

= =

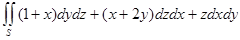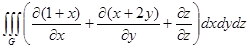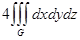
=[Перейдем к цилиндрическим координатам (r, t, z), в них множество G, задается неравенствами {0≤ r ≤2; 0≤ t ≤2π; r ²≤ z ≤4}] = 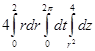= =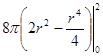32π

5. Используя формулу Стокса, вычислить интеграл:

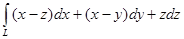, где L – окружность x ²+ y ²+z²=1, x+y+ z =1, ориентированная отрицательно, относительно вектора (0;0;1).

За поверхность S, ограниченную кривой L, примем часть секущей плоскости x+y+z=1, лежащей внутри сферы. Так как кривая ориентирована отрицательно, относительно вектора (0;0;1), то единичный вектор нормали должен быть направлен во внутрь сферы, см. 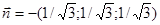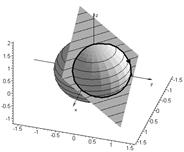рис.???,

рис.

Так как все функции P (x; y; z)= x - z, Q (x; y; z)= x-y, R (x; y; z)= z непрерывно дифференцируемы в

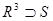то можно применить формулу Стокса.

Так как 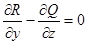, , 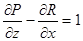, 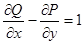получаем:

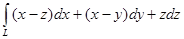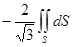= . S – есть круг, в плоскости x + y + z =1, так как вектор нормали 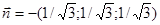, то расстояние от плоскости до начала координат равно 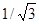. Значит множество S есть круг радиуса 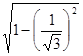= 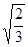, то есть = ,

=

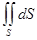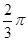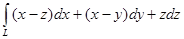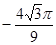
1. Найти поток поля 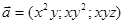через часть внешней стороны поверхности эллипсоида 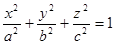, расположенную в первом октанте.

Поток векторного поля 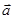через поверхность S в направлении внешней нормали равен интегралу: 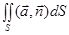. Поверхность S ограничивает множество V ={(x, y, z): 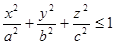}. Можно вычислить этот интеграл используя формулу Остроградского-Гаусса: = = =

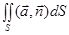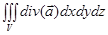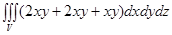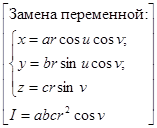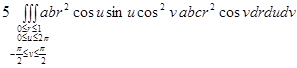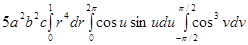= = =0