2015-09-06
1302
Для нахождения координат точек эвольвентного участка профиля впадины зубьев нарезаемого колесе введем прямоугольную систему координат Х' О' У'. При этом начало координат поместим в центр изделия О', а ось О'У' совместим с осью симметрии впадины между зубьями (рис.2.1.).
Тогда координаты произвольной точки Му эвольвенты впадины зуба находят по формулам:
Найдем диаметры фрезы:
d = m*z =8*34 = 272мм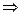 
r = 136мм
d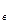 
= m*z*cos 
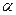= 8* 32* cos20 =255,6мм 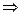r 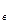= 127,8 мм
d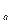 
= D+2m = 272+2*8= 292мм 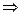r 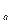= 146мм
r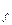 
= r- (1+c)*m =136-(1+0,25)*8 =126 мм
X' 
=r * sin 
(1)
У' = r * cos
где r - радиус произвольней точки;
- угол между радиусом-вектором, проведенным в точку иосью координат.
Угол определяют из уравнения.
= 
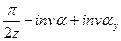(2)
= 
= 
= 
= 
= 
= 
= 
= 
= 
= 
= 
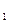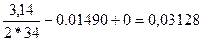
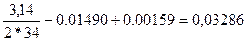
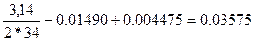
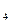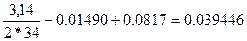
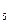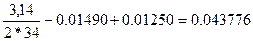
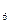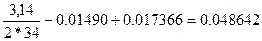
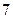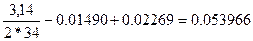
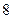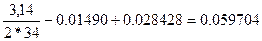
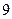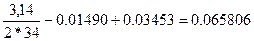
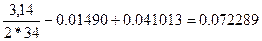
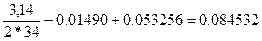
где 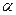inv и inv 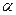- эвольвентные функции (инволюты этих углов)
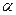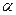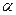inv = tg - (3)
Здесь угол 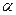в радианах.
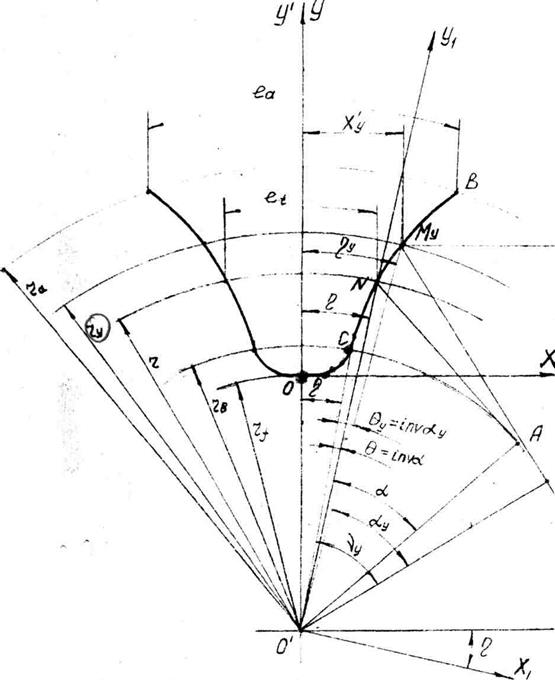
Рис.2.1 – Профилирование эвольвентного участка впадины зуба колеса
Угол давления в рассматриваемой точке Му профиля зубьев находят из выражения.
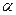
=arcos 
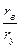
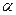
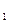= arcos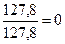 
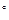
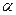
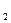= arcos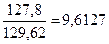 
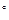
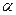
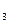= arcos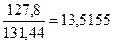 
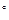
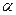
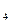= arcos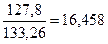 
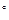
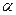
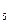= arcos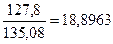 
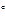
(4)
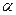
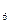= arcos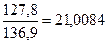 
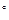
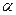
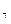= arcos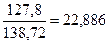 
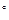
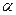
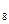= arcos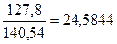 
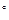
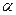
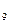= arcos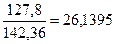 
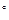
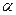
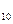= arcos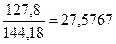 
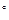
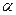
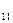= arcos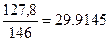 
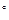
где 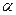в - радиус основной окружности.
Так как в данном случае начальная и основная окружности совпадают, то
r =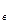 
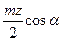(5)
Значения эвольвентных функций (инволют) даны в приложении А. Полученное в радианах значение , переводят в градусы.
= 
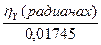(6)
y1=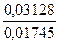 
=1, 7925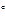
y2=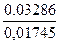 
=1, 8831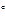
y3=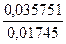 
=2, 0488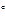
y4=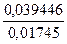 
=2.260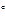5
y5=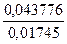 
=2.508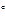6
y6=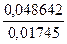 
=2, 7875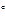
y7=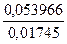 
=3.0926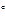
y8=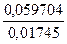 
=3, 4214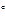
y9=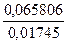 
=3, 7711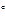
y10=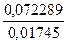 
=4, 1426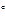
y11=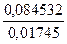 
=4, 8442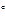
Для построения профиля шаблона введем новую систему координат Х' О' У'. Она отличается от старой системы X' О 'У ' смещением центра по оси О' У' на величину радиуса впадин зубьев колеса r 
. При этом направление осей обеих систем координат совпадают (рис.2.1).
Тогда координаты профиля шаблона для проверки эвольвентой части профиля впадины прямозубого цилиндрического колеса и соответствующего участка дисковой модульной фрезы находят по формулам:
х =r * sin (7)
у = r * cos -r
где r - радиус впадины зубьев нарезаемого колеса;
r = r-(1+c)*m(8)
где r - радиус делительной окружности колеса;
c -коэффициент радиального зазора зубчатой передачи,
с= 0,25
Найдем координаты точек профиля зуба фрезы из формулы (1).
х 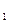= 127,8 * sin 1,7925 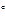= 3,9976
у 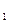= 127,8 * cos 1,7925 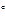= 127,7375
х 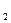= 129,62* sin 1,8831 = 4,2594
у 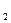= 129,62* cos 1,8831 = 129,55
х 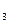= 131,44* sin 2,0488 = 4,699
у 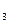= 131,44* cos 2,0488 = 130,699
х 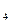= 133,25* sin 2.2605 = 5,2562
у 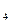= 133,25* cos 2.2605 = 133,156
х 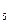= 135,08* sin 2.5086 = 5,9123
у 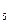= 135,08* cos 2.5086 =134,9505
х 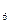= 136,9* sin 2,7875 = 6,6577
у 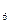= 136,9* cos 2,7875 = 136,748
х7=138,72* sin 3,0926=7,484
у7=138,72* cos 3,0926=138,518
х8=140,54* sin 3,4214=8,3873
у8=140,54* cos 3,4214 =140,2895
х9=142,36* sin 3,7711=9,363
у9=142,36* cos 3,7711 =142,0517
х10=144,18* sin 4,1426=10,415
у10=144,18* cos 4,1426 =143,803
х11=146* sin 4,8442=12,329
у11=146* cos 4,8442 =145,478
Найдём проекции участков PC и PD на ось OY, которые будут соответственно равны PB и PA по формулам:
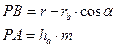(9)
где ha=1 – коэффициент высоты головки зуба. Подставив известные значения в формулы, получим:
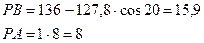
Положение точки K, являющейся нижней границей рабочего (активного) участка профиля зуба нарезаемого колеса находят по формуле:
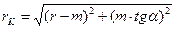(10)
подставив в формулу известные величины, получим:
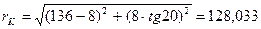
Так как 8=PA<PB=15,9 то профиль зуба может быть очерчен эвольвентой PK, прямой касательной к окружности впадин колеса OE и дугой сопряжения EK между ними.
При построении нерабочего участка профиля зуба нарезаемого колеса воспользуемся рекомендациями по ГОСТ 10996-64 с изменениями №2 к нему. По рекомендациям ГОСТ 10996-64 примем координаты точек для построения нерабочего участка профиля зуба:
XB=0,5292
YB=0,4255
XC=0,5386
YC=0,4685
XЦ=0
YЦ=0,5416
где XЦ и YЦ – координаты окружности, соединяющей два соседних зуба, XB, YB, XC, YC, φ – координаты начальной, конечной точек и угла наклона отрезка, соединяющего окружность с эвольвентным профилем.
