Комментарий
Попасть в кольцо можно разными способами, т. е. при различных комбинациях значений угла бросания 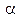 и начальной скорости Vo. Задача заключается в том, чтобы указать Vo при разных
и начальной скорости Vo. Задача заключается в том, чтобы указать Vo при разных 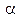 . Зная, что х =
. Зная, что х = 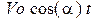 ; у =
; у = 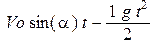 , найдем уравнение траектории.
, найдем уравнение траектории.
> sys:={x=Vo*cos(alpha)*t,y=Vo*sin(alpha)*t-(g*t^2)/2};
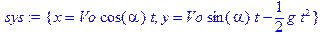
> solve(sys, {y,t});
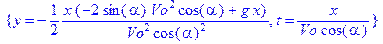
Закон движения
> y:=1/2*x*(2*sin(alpha)*Vo^2*cos(alpha)-g*x)/Vo^2/cos(alpha)^2;
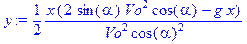
Подставив х = l, у = h, выведем связь между углом бросания 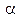 и необходимой скоростью Vo.
и необходимой скоростью Vo.
> y:=h; x:=l;
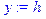
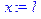
> О:=-h+1/2*x*(2*sin(alpha)*Vo^2*cos(alpha)-g*x)/Vo^2/cos(alpha)^2;
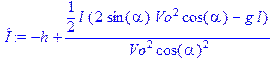
> Vo:=solve(О,Vo);
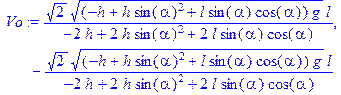
Для дальнейшего решения задачи нам необходимо только положительное значение Vo, поэтому мы будем пользоваться только первым корнем.
> Vo:=%[1];
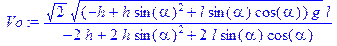
> Vo:=1/(-2*h+2*h*sin(alpha*3.14/180)^2+2*l*sin(alpha*3.14/180)*cos(alpha*3.14/180))*2^(1/2)*((-h+h*sin(alpha*3.14/180)^2+l*sin(alpha*3.14/180)*cos(alpha*3.14/180))*g)^(1/2)*l;
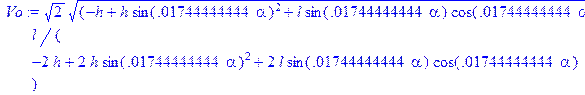
 2015-09-06
2015-09-06 159
159







