Задача визначення мінімального радіуса кулачка розв’язується так.
1. На підставі побудованих діаграм 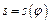 і
і 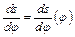 будуємо діаграму
будуємо діаграму 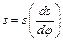 . Для цього на осі ординат відкладаємо переміщення
. Для цього на осі ординат відкладаємо переміщення 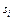 штовхача, а на осі абсцис – відповідні їм значення аналогів швидкостей
штовхача, а на осі абсцис – відповідні їм значення аналогів швидкостей 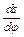 . Масштаби на осі ординат і осі абсцис однакові
. Масштаби на осі ординат і осі абсцис однакові 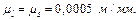
2. З’єднуючи одержані точки 1, 2, 3 і т. д. (див. аркуш 2 (додаток Б)), отримаємо діаграму 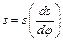 у вигляді замкненої кривої.
у вигляді замкненої кривої.
3. Проводимо під кутом 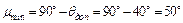 до осі
до осі 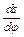 дві
дві
дотичні до побудованої кривої 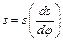 , які обмежують певну частину площини (на аркуші 2 (додаток Б) вона заштрихована). Будь-яка точка, що лежить у цій площині може бути центром обертання кулачка.
, які обмежують певну частину площини (на аркуші 2 (додаток Б) вона заштрихована). Будь-яка точка, що лежить у цій площині може бути центром обертання кулачка.
4. Відкладаємо зміщення центра обертання кулачка відносно осі штовхача (вісь штовхача на діаграмі 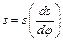 збігається з віссю
збігається з віссю 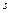 ), яке
), яке
на кресленні визначається відрізком 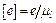 , де
, де 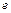 – ексцентриситет штовхача, мм. У нашому випадку
– ексцентриситет штовхача, мм. У нашому випадку 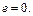
Отже, центр обертання кулачка може бути вибраний у будь-якій точці 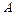 , яка знаходиться у заштрихованій зоні на осі штовхача. Приймаємо відрізок
, яка знаходиться у заштрихованій зоні на осі штовхача. Приймаємо відрізок 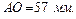 Тоді мінімальний радіус кулачка:
Тоді мінімальний радіус кулачка:
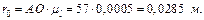
Приймаємо 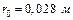 або
або 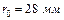 .
.
 2015-09-06
2015-09-06 319
319








