Второе начало термодинамики

Не все не противоречащие закону сохранения энергии процессы, могут происходить в реальности. Причины, по которым процесс может идти в одном направлении и не может в другом, объясняет II начало термодинамики, для которого есть несколько формулировок.

1. Клаузиус (1850): невозможен самопроизвольный переход тепла от менее к более нагретому телу, или невозможны процессы, единственным конечным результатом которых был бы переход тепла от менее нагретого тела к более нагретому.

Работа обычного холодильника не противоречит этому утверждению, так как для его работы требуется еще энергия извне (электрическая). Поэтому понижение температуры внутри холодильника и повышение её снаружи не является единственным результатом работы холодильника. Не включенный в сеть холодильник, как известно, не работает.

2. Кельвин (1851): невозможны процессы, единственным конечным результатом которых было бы превращение тепла целиком в работу.

Пример. Пусть газ изотермически расширился. Внутренняя энергия не изменилась, так как температура осталось прежней, а все полученное тепло перешло в работу. Однако это не единственный результат: в частности, изменился объем. 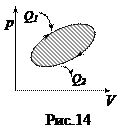Можно показать, что формулировки 1. и 2. эквивалентны: из первой следует вторая и наоборот. Если бы не второе начало, можно было бы легко решить энергетические проблемы – построить двигатель, который отнимал бы тепло из океанов и целиком превращал его в работу (перпетуум-мобиле II-го рода). Это позволяет перефразировать формулировку Кельвина так: перпетуум-мобиле II -го рода невозможен, или невозможно создать тепловой двигатель с КПД =1.

Коэффициент полезного действия тепловой машины (КПД). Любой тепловой двигатель работает по замкнутому циклу (рис.14). Если процесс совершается по часовой стрелке, то работа за цикл положительна. Если на каких-то этапах рабочему телу (газу) сообщается тепло Q ₁, то, чтобы вернуться в исходное состояние газ должен на других участках цикла отдать холодильнику тепло Q ₂. По I началу термодинамики приращение внутренней энергии за цикл = 0, так как система вернулась в исходное состояние, а внутренняя энергия есть функция состояния. Поэтому, работа за цикл А = Q ₁- Q ₂. КПД теплового двигателя определяется как отношение полезной работы А к полученному теплу Q ₁, Þ

h = 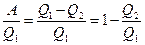. (51)

h =1 запрещено II-м началом термодинамики. Опыт также показывает, что h <1.

Необратимость процессов. Все процессы в макросистемах являются необратимыми. Обратимые процессы – это идеализация, удобная для решения многих важных вопросов. В чем причина необратимости? Необратимость выглядит особенно странно, если учесть, что все законы механики обратимы во времени. И, тем не менее, никто не видел, чтобы, например, разбившаяся ваза самопроизвольно восстановилась из осколков. Загадочны и запреты, устанавливаемые вторым началом термодинамики. Решение этой сложной проблемы пришло с открытием новой термодинамической величины – энтропии - и раскрытием её физического смысла.

Энтропия. По Клаузиусу, энтропия вводится через её элементарное приращение

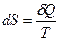. (51)

Как известно, 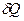не является дифференциалом функции, но после деления на температуру получается полный дифференциал! В отличие от теплоты, энтропия 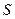является такой же функцией состояния как температура, внутренняя энергия или давление. Полученное системой тепло Q зависит от процесса перехода из начального состояния в конечное. Приращение энтропии D S совершенно не зависит от процесса, а только от начального и конечного состояний. В интегральной форме соотношение (51) принимает вид

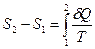, (52)

причем совершенно не важно, какой процесс произошел между состояниями 1 и 2, этот процесс может быть даже необратимым, важно лишь, чтобы состояния 1 и 2 были равновесными. Знак равенства в (51) и (52) относится только к квазистатическим (равновесным) процессам. В остальных случаях знак "=" заменяется на знак " > ". Это значит, при неравновесных процессах энтропия получает ещё дополнительное приращение, обусловленное самой необратимостью процесса. Следует добавить, что определение энтропии по формулам (51) и (52) позволяет вычислить только изменение энтропии, но не её абсолютное значение. Это значит, что энтропия определена с точностью до константы. Перечислим некоторые свойства энтропии.

1. Энтропия – функция состояния. Если процесс адиабатический, то Q =0, Þ энтропия остается постоянной.

2. Энтропия аддитивна: энтропия макросистемы равна сумме энтропий её отдельных частей.

3. Несколько позднее мы получим еще одно свойство: энтропия S характеризует степень беспорядка в макросистеме: состояниям с большим беспорядком отвечает большее значение энтропии

Принцип возрастания энтропии замкнутых систем является еще одной формулировкой II-го начала термодинамики: энтропия замкнутой (теплоизолированной) системы не уменьшается – она либо возрастает, либо остается постоянной.

Величина возрастания энтропии в замкнутой макросистеме может служить мерой необратимости процессов. В пределе, когда процессы обратимы, энтропия замкнутой системы остается постоянной. Оказывается, все самопроизвольно и в изолированных условиях протекающие в природе процессы протекают с возрастанием энтропии. Необходимо специальное взаимодействие с окружающей средой, чтобы препятствовать возрастанию энтропии в макросистеме. Ярким примером могут служить все живые существа.

Примеры применения энтропии.

1.Уравнение I-го начала термодинамики с помощью энтропии можно переписать так:

TdS = dU + pdV. (53)

2. Энтропия идеального газа. Разделим (53) на Т подставим для 1 моля газа :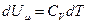

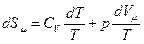. Из уравнения состояния для 1 моля газа (pV_m=RT) найдем 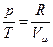и подставим во второе слагаемое:

.

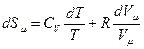Дифференциал от логарифма уравнения (pV_m=RT) есть 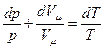, поэтому

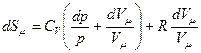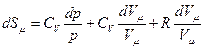, Þ 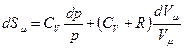, Þ

, Þ

.

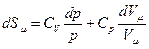Проинтегрируем это уравнение между двумя состояниями 1 и 2:

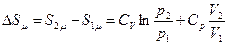. (54)

Вследствие аддитивности энтропии, приращение энтропии для ν молей газа будет в ν раз больше.

3. Возрастание энтропии при смешении газов. Пусть в двух половинках теплоизолированного сосуда находятся одинаковые количества двух различных идеальных газов. После удаления перегородки начнется необратимый процесс смешивания газов. Процесс закончится, когда газы будут равномерно перемешаны, т.е. система перейдет в равновесное состояние при той же температуре. Рассмотрим процессы изотермического распространения каждого газа в чужую половинку, как независимые. Изменение энтропии для одного из них равно 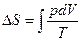, так как внутренняя энергия не изменилась, Þ 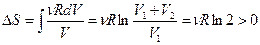, Þ энтропия возрастает, и окончательно 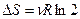. Вследствие аддитивности энтропии, приращение энтропии для двух газов в два раза больше: .

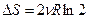Цикл Карно. Тепловой двигатель Карно состоял из нагревателя с температурой 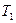, холодильника с температурой 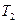и рабочего тела (идеального газа в цилиндре под поршнем), способного получать тепло и совершать работу. Карно рассмотрел цикл (рис.15) из двух изотерм (ab и cd) и двух адиабат (bc и da). При изотермическом расширении (ab) газ находится в контакте с нагревателем при температуре 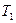, и получает тепло Q ₁. При изотермическом сжатии (cd) газ находится в контакте с холодильником при температуре 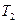, и отдает холодильнику Q ₂. В соответствии с (51) КПД теплового двигателя равно

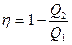. (55)

Цикл Карно является обратимым, т.е. он может быть проведен бесконечно медленно в обратном направлении и при этом газ совершит отрицательную работу, холодильник отдаст газу тепло Q ₂, нагреватель получит обратно тепло Q ₁. Именно так работает холодильник.

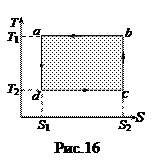
Дальнейшие рассуждения о цикле Карно удобнее проводить в координатах T-S (температура-энтропия), когда цикл изображается прямоугольником (рис.16). В этим случае изотермы изображаются прямыми ab и cd, адиабаты – отрезками bc и da. В соответствии с (52) 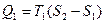и равно площади под отрезком ab. Отданное холодильнику тепло 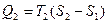и равно площади под отрезком cd. Площадь прямоугольника, равная Q ₁- Q ₂, есть работа А, совершаемая двигателем за цикл. Подставив выражения для Q ₁и Q ₂ в (55), получим КПД цикла Карно

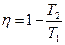. (56)

Полученный вывод составляет содержание знаменитой теоремы Карно: КПД обратимых двигателей, работающих по циклу Карно, зависит только от температур 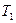и 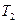- нагревателя и холодильника, но не зависит ни от устройства двигателя, ни от рода рабочего вещества.

Статистический смысл второго начала термодинамики. Если состояние макросистемы охарактеризовано такими параметрами, как объем, давление, число молей и т.д. говорят, что задано макросостояние. Если состояние макросистемы задано настолько подробно, что указаны положения всех её частиц, то говорят, что задано микросостояние. Любое макросостояние может быть реализовано многими различными способами. Число различных микросостояний, которыми может быть реализовано данное макросостояние называется статистическим весом этого макросостояния.

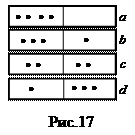
Пример. Пусть в сосуде, разделенном пополам, могут разместиться 4 молекулы. Варианты размещений представлены на рис.17. Пронумеруем молекулы. Каждая из них с равной вероятностью может находиться в каждой половине. Значит, вероятность того, что любая молекула окажется слева равна ½. Пребывание в левой половинке двух молекул – события независимые, поэтому вероятность равна произведению: 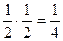; трех молекул - 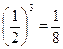; четырех молекул - 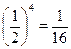. Рассуждая аналогично, легко понять, что любое размещение 4-х молекул по двум ячейкам имеет вероятность 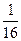. Каждое размещение соответствует одному микросостоянию, которые все перечислены в таблице 1.

Таблица 1

Способы реализации микросостояний	Число способов (статистич. вес) Ω	Обычная вероятность Р
В левой половине	В правой половине
-	1,2,3,4,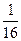
	2,3,4 1,3,4 1,2,4 1,2,3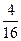
1,2 1,3 1,4 2,3 2,4 3,4	3,4 2,4 2,3 1,4 1,3 1,2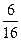
1,2,3 1,2,4 1,3,4 2,3,4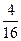
1,2,3,4	-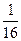

Всего микросостояний 2⁴ =16.

Поскольку для характеристики макросостояния не важно, какие именно из 4-х молекул находятся, например, слева, а важно сколько их, то макросостояние характеризуется числом молекул в половинках слева и справа (аналог концентрации, параметра макросостояния). Всего различных макросостояний пять, и каждому из них соответствует свое число микросостояний (т.е. свой статистический вес Ω). Например, макросостоянию состоящему в том, что в каждой половине сосуда находятся по две молекулы отвечает статистический вес Ω =6, а его вероятность Р = 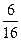. Это наиболее вероятное макросостояние. Для N частиц по аналогии с нашим примером вероятность каждого микросостояния будет равна 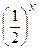, а полное число микросостояний 2 ^N. При N =10²⁰ вероятность каждого микросостояния невообразимо мала: 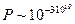. Это значит, что макросостояния с небольшим статистическим весом, например все молекулы – в левой части сосуда, становятся практически неосушествимым.

Таким образом, мы пришли к важному выводу: предоставленная самой себе макросистема стремится переходить от менее вероятных макросостояний к более вероятным. В этом суть необратимости. Второе начало термодинамики, указывающее на необратимость перехода работы в тепло, обусловлено тем, что обратный переход означал бы переход от более вероятного состояния к менее вероятному.

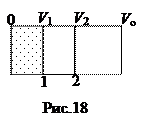
Энтропия и вероятность. Если макросистема находится в неравновесном состоянии, то она будет переходить в состояние с большей вероятностью – вплоть до равновесия. Вместе с тем, согласно второму началу термодинамики все самопроизвольные процессы в замкнутой макро-системе сопровождаются возрастанием энтропии. Поэтому следует ожидать, что между энтропией макросистемы в каждом состоянии и вероятностью в том же состоянии должна существовать связь (идея Больцмана). Чтобы найти эту связь рассмотрим необратимый процесс расширения идеального газа в пустоту. Пусть сначала газ находился в объеме V ₁ теплоизолированного сосуда объемом V _o, который разделен перегородками 1 и 2 на три части (рис.18). Допустим, перегородку мгновенно перемещают из положения 1 в положение 2, газ расширяется до объема V ₂ и приходит в равновесное состояние. Так как газ при этом работу не совершает (А =0), и (Q= 0), Þ и D U =0: температура газа не меняется. Поскольку энтропия – функция состояния, то ее приращение между состояниями 1 и 2 можно вычислить все равно по какому обратимому процессу, например, изотермическому, хотя во всех остальных отношениях этот процесс протекает по-другому: совершается работа, передается тепло и т.д. В изотермическом процессе

Q = А = 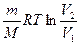(см. (22));

Þ D S = = = .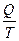

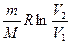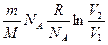Поскольку 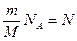- полному числу молекул, а 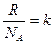, т.е. постоянной Больцмана, то

D S = 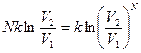. (57)

В состояниях 1 и 2 распределение по скоростям должно быть одинаковым, так как масса газа и его температура остались прежними. Но в конечном состоянии молекулы стали располагаться просторнее, значит оно более вероятно. Вероятность нахождения одной молекулы в объеме V ₁ равна 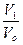, а всех молекул Р ₁= 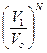. Аналогично, вероятность нахождения всех молекул в объеме V ₂ равна Р ₂= 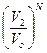, а отношение вероятностей .

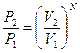Подставляя в (57), получим D S = 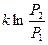. Поскольку вероятность макросостояния пропорциональ-на его статистическому весу, то 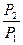= 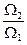, Þ

D S = 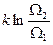. (58)

Так мы пришли к знаменитой формуле Больцмана:

S = 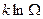. (59)

Логарифм в формуле Больцмана - исключительная удача. Ведь логарифм произведения равен сумме логарифмов, что соответствует свойству аддитивности энтропии.

Теперь очевидна и связь энтропии и вероятности (или стат. веса): раз все процессы идут в направлении возрастания Р (и Ω), следовательно, в соответствии с формулой (59) они идут в направлении возрастания энтропии. Принцип возрастания энтропии привел Больцмана к фундаментальному выводу: все замкнутые макросистемы стремятся переходить от состояний менее вероятных к состояниям более вероятным. При этом сама энтропия S характеризует степень беспорядка в макросистеме: состояниям с большим беспорядком отвечает большая вероятность (и Ω) и большее значение энтропии. Именно поэтому и возникает необратимость реальных самопроизвольных процессов. Любой вид энергии в конце концов переходит во внутреннюю энергию, т.е. в равновесное состояние, при котором «хаос» максимален – это состояние с максимальной энтропией.