Розглянемо спочатку ствердження (3) для натурального значення аргументу, а саме доведемо, що границя послідовності з загальним членом 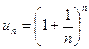 ,
,
якщо 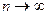 дорівнює:
дорівнює:
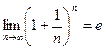 . (4)
. (4)
Проведемо аналіз поведінки послідовності з загальним членом 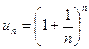 при
при 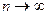 . Доведемо, що послідовність
. Доведемо, що послідовність 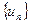 монотонно зростає. Дійсно, скористаємося формулою бінома Ньютона
монотонно зростає. Дійсно, скористаємося формулою бінома Ньютона
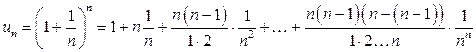
або
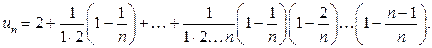
Із зростанням 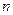 зростає як число додатних доданків, так і величина кожного доданка, тобто послідовність
зростає як число додатних доданків, так і величина кожного доданка, тобто послідовність 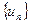 зростає.
зростає.
Зробимо оцінку загального члена послідовності 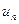 :
:
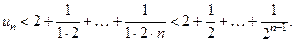
Отже, маємо суму 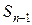 членів геометричної прогресії з першим членом
членів геометричної прогресії з першим членом 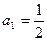 та знаменником
та знаменником 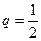 .
.
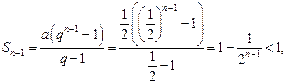
або 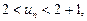 тобто
тобто 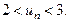
Отже, послідовність 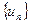 монотонно зростає і обмежена., тобто має границю. Границя числової послідовності
монотонно зростає і обмежена., тобто має границю. Границя числової послідовності 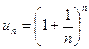 дорівнює ірраціональному числу
дорівнює ірраціональному числу 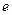
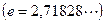
Можна довести, що функція 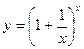 при
при 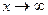 також має границю, яка дорівнює
також має границю, яка дорівнює 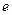 .
.
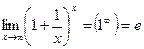 (5)
(5)
Останню рівність можна записати і в такому вигляді:
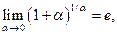 (6)
(6)
де 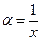 , при
, при 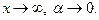
 2015-09-06
2015-09-06 302
302







