Тема Перша та друга важливі границі
Перша важлива границя.
Область застосування першої важливоїграниці – розкриття невизначеності «нуль на нуль», яка породжується функціями, що містять як складову частину тригонометричні або обернені тригонометричні функції.
Теорема. Границя відношення синуса нескінченно малого аргументу до цього ж аргументу дорівнює одиниці:
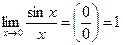 . (1)
. (1)
Доведення.
Щоб довести теорему, розглянемо коло одиничного радіуса з центром у початку координат − точці  (рис. 1).
(рис. 1).
 Рис. 1. Чверть тригонометричного круга Рис. 1. Чверть тригонометричного круга | Візьмемо гострий кут 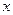 у першій чверті тригонометричного круга, тобто у першій чверті тригонометричного круга, тобто 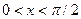 , де , де 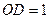 , , 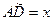 , ,  , , 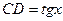 . Порівнюючи площі трикутника . Порівнюючи площі трикутника 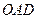 , кругового сектора , кругового сектора 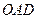 і трикутника і трикутника 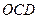 , отримуємо: , отримуємо: 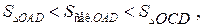 |
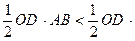
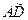
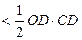
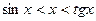 Þ
Þ 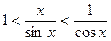 .
.
Замінюємо члени нерівності оберненими величинами і, з урахуванням умови 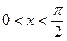 , одержуємо нерівність:
, одержуємо нерівність: 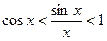 .
.
Зауважимо, що дані нерівності виконуються і для 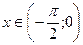 , тому що функції
, тому що функції 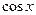 і
і 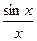 - парні. Переходячи до границі при
- парні. Переходячи до границі при 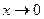 , будемо мати:
, будемо мати:
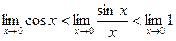 Þ
Þ 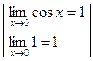 Þ
Þ 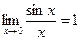 .
.
Таким чином, для границі справа співвідношення (1) доведено. Для лівосторонньої границі, коли 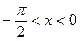 , в силу парності функцій
, в силу парності функцій 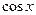 та
та 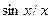 приходимо до того ж результату, адже
приходимо до того ж результату, адже 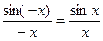 .
.
Зауважимо, що аргументом під знаком синуса може бути довільна нескінченно мала 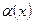 при
при 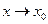 . Отже, маємо узагальнення формули (1):
. Отже, маємо узагальнення формули (1):
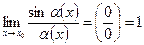 . (2)
. (2)
Друга важлива границя.
Область застосування другої важливої границі – розкриття невизначеності «одиниця у степені нескінченність», яка породжується степенево-показниковими функціями 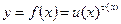 .
.
Теорема. Границя степенево-показникової функції при прямуванні аргументу 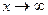 ,
, 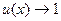 ,
, 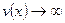 дорівнює числу
дорівнює числу 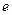 :
:
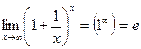 . (3)
. (3)
 2015-09-06
2015-09-06 1154
1154







