Задание 1
1. Начертить область интегрирования, изменить порядок интегрирования.
2. Вычислить.
3. Найти центр тяжести однородной фигуры, ограниченной данными линиями.
4. Найти объем тела, заданного ограничивающими его поверхностями.
5. Перейдя к полярным координатам, вычислить.
6. Нарисовать тело, объем которого описывается данным интегралом. Объем сосчитать.
7. Пластинка D задана ограничивающими ее кривыми, m - поверхностная плотность.
Найти массу пластинки.
1.1 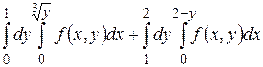 .
.
1.2 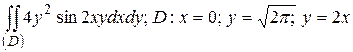 .
.
1.3 x=y2; x=4.
1.4 x2+y2=50; y= 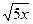 ; y=0; z=0; z=
; y=0; z=0; z= 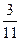 x.
x.
1.5 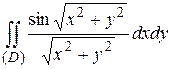 ;
; 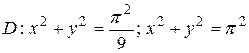 .
.
1.6 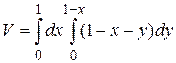 .
.
1.7 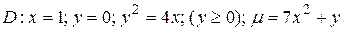 .
.
2.1 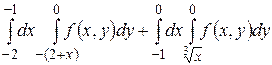 .
.
2.2 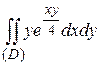 ; D: y=ln2; y=ln3; x=4; x=8.
; D: y=ln2; y=ln3; x=4; x=8.
2.3 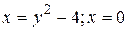 .
.
2.4 x= 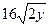 ; x=
; x= 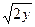 ; z+y=2; z=0.
; z+y=2; z=0.
2.5 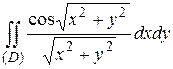 ;
; 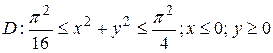 .
.
2.6 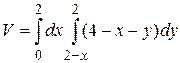 .
.
2.7 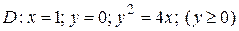 ;
; 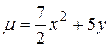 .
.
3.1 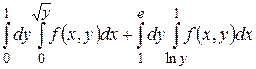 .
.
3.2 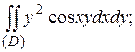 D: x=0; y=
D: x=0; y= 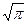 ; y=x.
; y=x.
3.3 x =4 –y2; x=0.
3.4 x+y=8; y= 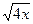 ; z=3y; z=0.
; z=3y; z=0.
3.5 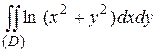 ;
; 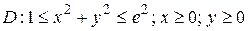 .
.
3.6 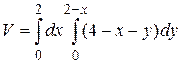 .
.
3.7 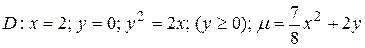 .
.
4.1 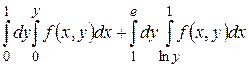 .
.
4.2 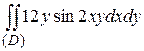 ; D: y=
; D: y= 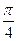 ; y=
; y= 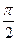 ; x=2; x=3.
; x=2; x=3.
4.3 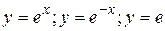 .
.
4.4 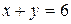 ;
; 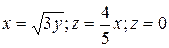 .
.
4.5 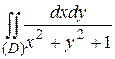 ;
; 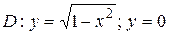 .
.
4.6 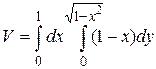 .
.
4.7 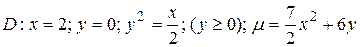 .
.
5.1 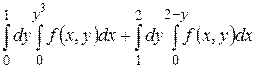 .
.
5.2 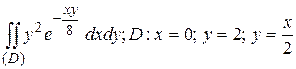 .
.
5.3 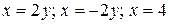 .
.
5.4 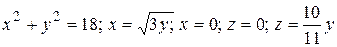 .
.
5.5 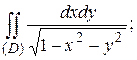
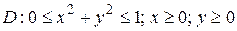 .
.
5.6 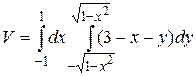 .
.
5.7 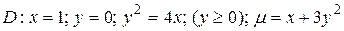 .
.
6.1 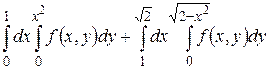 .
.
6.2 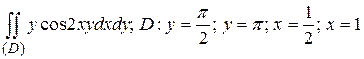 .
.
6.3 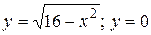 .
.
6.4 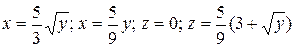 .
.
6.5 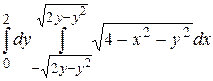 .
.
6.6 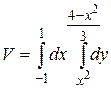 .
.
6.7 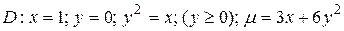 .
.
7.1 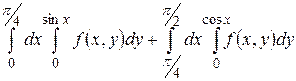 .
.
7.2 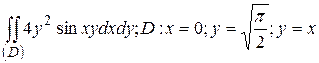 .
.
7.3 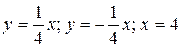 .
.
7.4 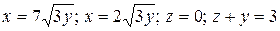 .
.
7.5 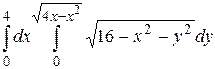 .
.
7.6 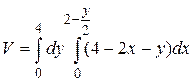 .
.
7.7 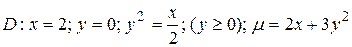 .
.
8.1 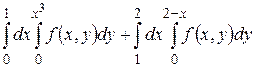 .
.
8.2 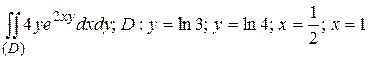 .
.
8.3 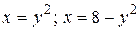 .
.
8.4 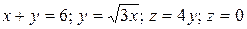 .
.
8.5 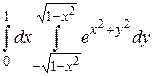 .
.
8.6 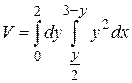 .
.
8.7 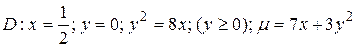 .
.
9.1 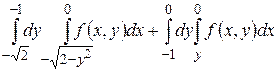 .
.
9.2 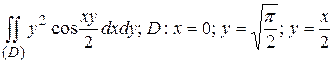 .
.
9.3 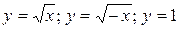 .
.
9.4 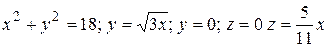 .
.
9.5 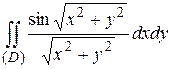 ;
; 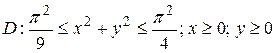 .
.
9.6 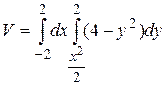 .
.
9.7 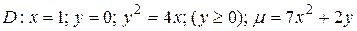 .
.
10.1 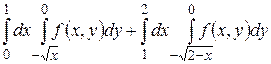 .
.
10.2 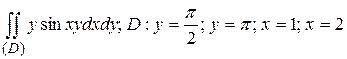 .
.
10.3 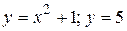 .
.
10.4 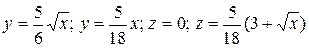 .
.
10.5 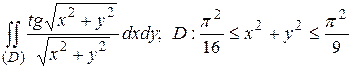 .
.
10.6 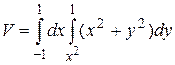 .
.
10.7 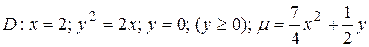 .
.
11.1 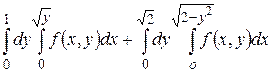 .
.
11.2 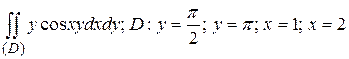 .
.
11.3 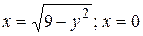 .
.
11.4 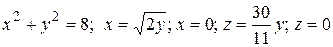 .
.
11.5 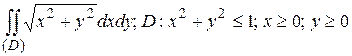 .
.
11.6 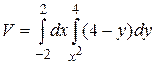 .
.
11.7 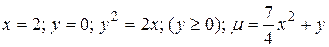 .
.
12.1 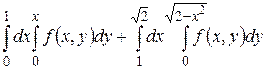 .
.
12.2 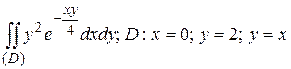 .
.
12.3 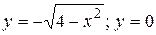 .
.
12.4 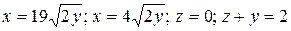 .
.
12.5 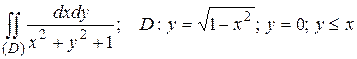 .
.
12.6 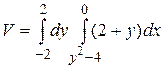 .
.
12.7 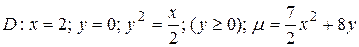 .
.
13.1 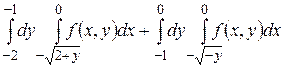 .
.
13.2 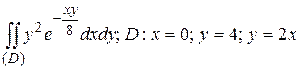 .
.
13.3 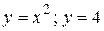 .
.
13.4 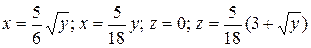 .
.
13.5 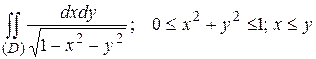 .
.
13.6 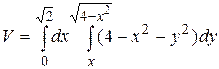 .
.
13.7 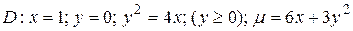 .
.
14.1 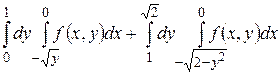 .
.
14.2 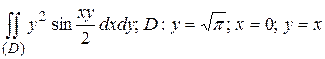 .
.
14.3 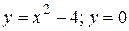 .
.
14.4 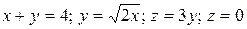 .
.
14.5 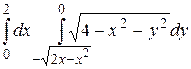 .
.
14.6 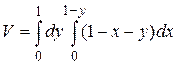 .
.
14.7 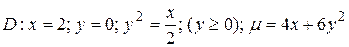 .
.
15.1 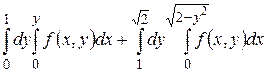 .
.
15.2 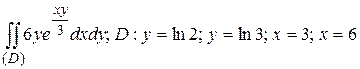 .
.
15.3 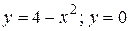 .
.
15.4 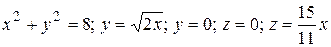 .
.
15.5 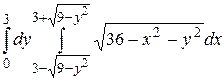 .
.
15.6 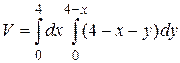 .
.
15.7 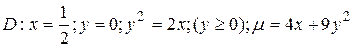 .
.
16.1 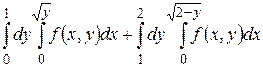 .
.
16.2 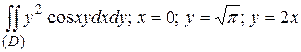 .
.
16.3 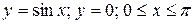 .
.
16.4 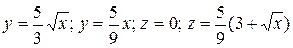 .
.
16.5 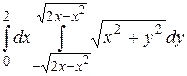 .
.
16.6 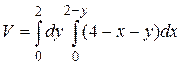 .
.
16.7 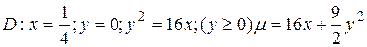 .
.
17.1 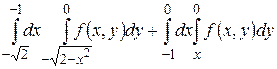 .
.
17.2 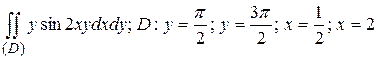 .
.
17.3 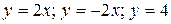 .
.
17.4 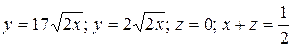 .
.
17.5 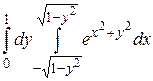 .
.
17.6 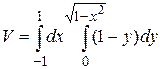 .
.
17.7 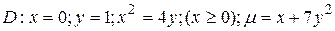 .
.
18.1 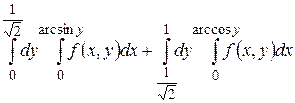 .
.
18.2 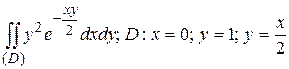 .
.
18.3 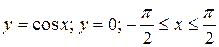 .
.
18.4 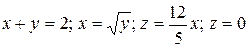 .
.
18.5 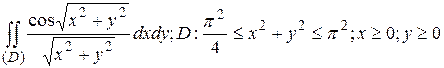 .
.
18.6 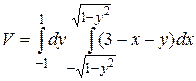 .
.
18.7 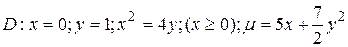 .
.
19.1 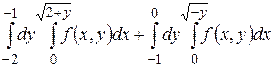 .
.
19.2 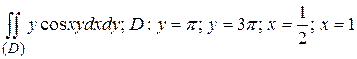 .
.
19.3 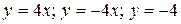 .
.
19.4 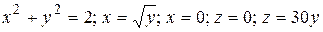 .
.
19.5 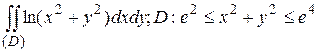 .
.
19.6 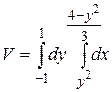 .
.
19.7 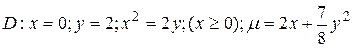 .
.
20.1 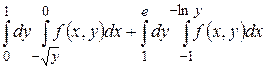 .
.
20.2 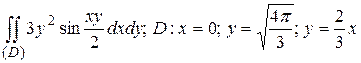 .
.
20.3 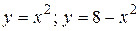 .
.
20.4 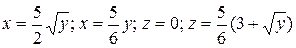 .
.
20.5 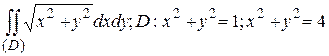 .
.
20.6 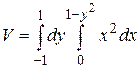 .
.
20.7 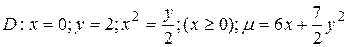 .
.
21.1 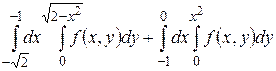 .
.
21.2 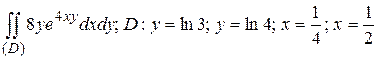 .
.
21.3 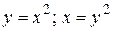 .
.
21.4 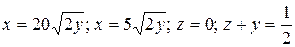 .
.
21.5 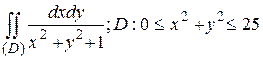 .
.
21.6 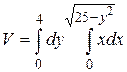 .
.
21.7 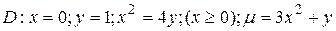 .
.
22.1 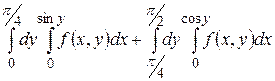 .
.
22.2 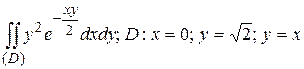 .
.
22.3 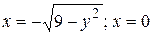 .
.
22.4 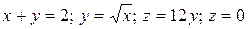 .
.
22.5 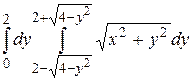 .
.
22.6 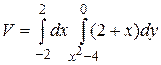 .
.
22.7 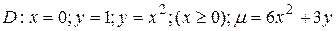 .
.
23.1 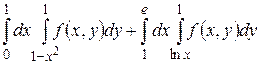 .
.
23.2 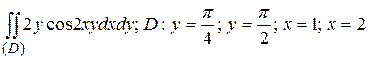 .
.
23.3 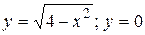 .
.
23.4 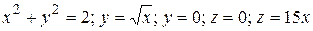 .
.
23.5 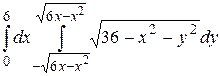 .
.
23.6 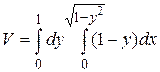 .
.
23.7 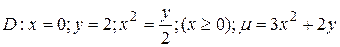 .
.
24.1 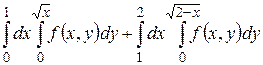 .
.
24.2 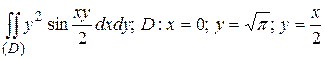 .
.
24.3 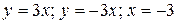 .
.
24.4 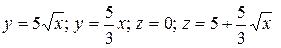 .
.
24.5 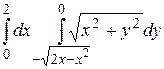 .
.
24.6 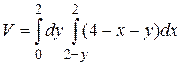 .
.
24.7 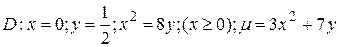 .
.
25.1 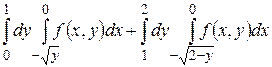 .
.
25.2 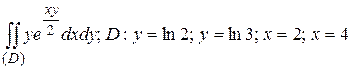 .
.
25.3 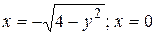 .
.
25.4 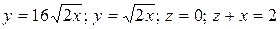 .
.
25.5 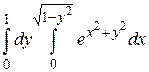 .
.
25.6 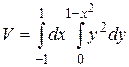 .
.
25.7 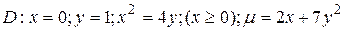 .
.
26.1 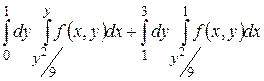 .
.
26.2 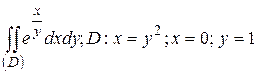 .
.
26.3 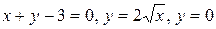 .
.
26.4 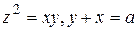 .
.
26.5 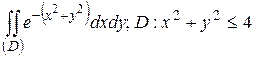 .
.
26.6 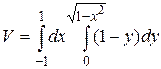
 .
.
26.7 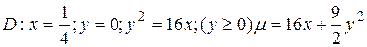 .
.
27.1 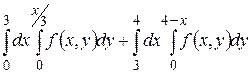 .
.
27.2 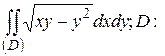 треугольник с вершинами
треугольник с вершинами 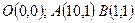 .
.
27.3 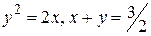 .
.
27.4 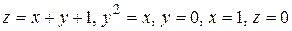 .
.
27.5 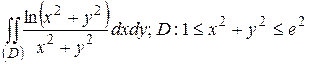 .
.
27.6 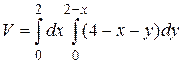 .
.
27.7 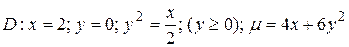 .
.
28.1 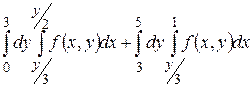 .
.
28.2 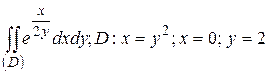 .
.
28.3 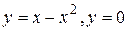 .
.
28.4 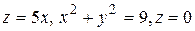 .
.
28.5 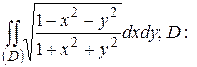
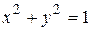 ,
, 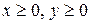 .
.
28.6 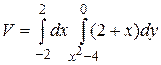 .
.
28.7 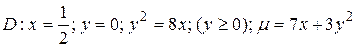 .
.
29.1 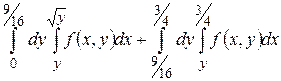 .
.
29.2 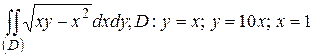 .
.
29.3 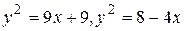 .
.
29.4 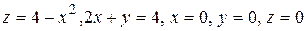 .
.
29.5 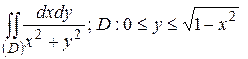 .
.
29.6 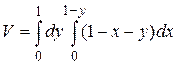 .
.
29.7 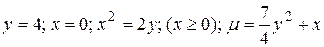 .
.
30.1 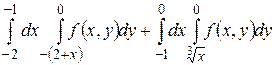 .
.
30.2 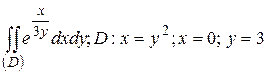 .
.
30.3 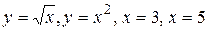 .
.
30.4 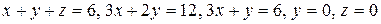 .
.
30.5 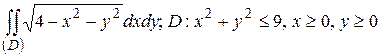 .
.
30.6 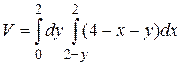 .
.
30.7 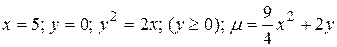 .
.
Задание 2
7 Найти работу силы 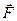 при перемещении вдоль линии
при перемещении вдоль линии 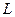 от точки
от точки 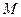 к
к 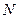 .
.
8 Вычислить интеграл двумя способами: непосредственно и по формуле Грина. 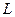 -контур многоугольника
-контур многоугольника 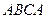 или
или 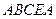 .
.
9 Доказать, что данное выражение является полным дифференциалом, найти первообразную. Сделать проверку.
1.8 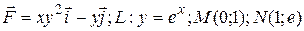 .
.
1.9 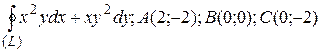 .
.
1.10 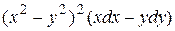 .
.
2.8 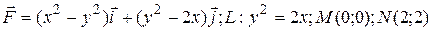 .
.
2.9 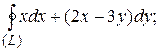
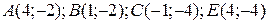 .
.
2.10 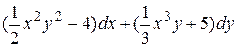 .
.
3.8 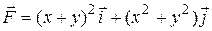 ;
; 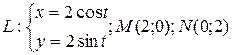 .
.
3.9 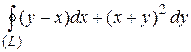 ;
; 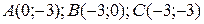 .
.
3.10 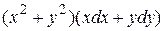 .
.
4.8 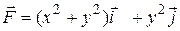 ;
; 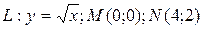 .
.
4.9 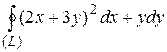 ;
; 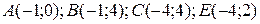 .
.
4.10 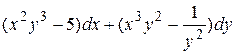 .
.
5.8 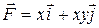 ;
; 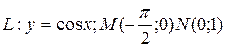 .
.
5.9 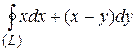 ;
; 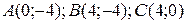 .
.
5.10 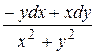 .
.
6.8 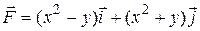 ;
; 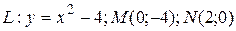 .
.
6.9 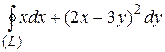 ;
; 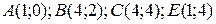 .
.
6.10 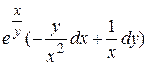 .
.
7.8 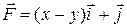 ;
; 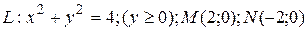 .
.
7.9 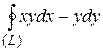 ;
; 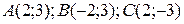 .
.
7.10 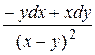 .
.
8.8 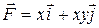 ;
; 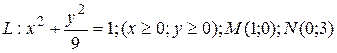 .
.
8.9 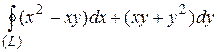 ;
; 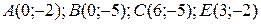 .
.
8.10 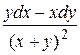 .
.
9.8 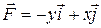 ;
; 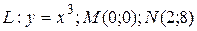 .
.
9.9 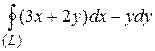 ;
; 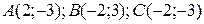 .
.
9.10 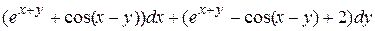 .
.
10.8 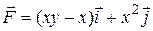 ;
; 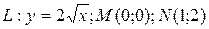 .
.
10.9 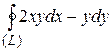 ;
; 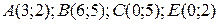 .
.
10.10 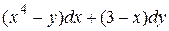 .
.
11.8 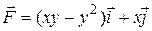 ;
; 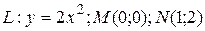 .
.
11.9 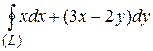 ;
; 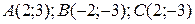 .
.
11.10 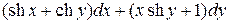 .
.
12.8 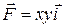 ;
; 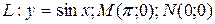 .
.
12.9 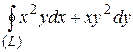 ;
; 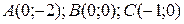 .
.
12.10 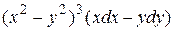 .
.
13.8 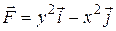 ;
; 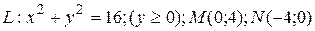 .
.
13.9 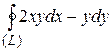 ;
; 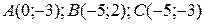 .
.
13.10 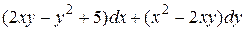 .
.
14.8 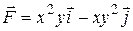 ;
; 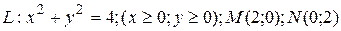 .
.
14.9 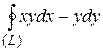 ;
; 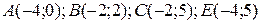 .
.
14.10 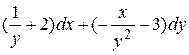 .
.
15.8 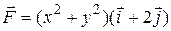 ;
; 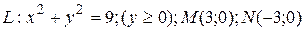 .
.
15.9 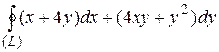 ;
; 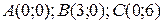 .
.
15.10 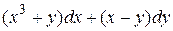 .
.
16.8 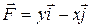 ;
; 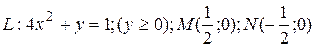 .
.
16.9 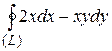 ;
; 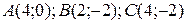 .
.
16.10 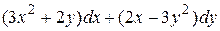 .
.
17.8 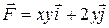 ;
; 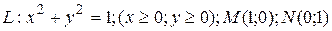 .
.
17.9 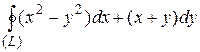 ;
; 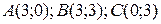 .
.
17.10 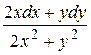 .
.
18.8 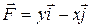 ;
; 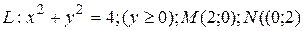 .
.
18.9 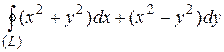 ;
; 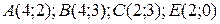 .
.
18.10 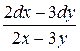 .
.
19.8 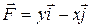 ;
; 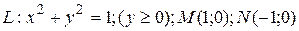 .
.
19.9 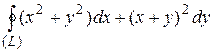 ;
; 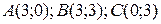 .
.
19.10 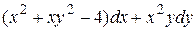 .
.
20.8 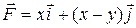 ;
; 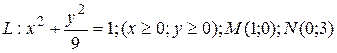 .
.
20.9 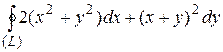 ;
; 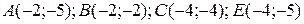 .
.
20.10 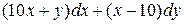 .
.
21.8 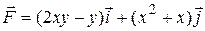 ;
; 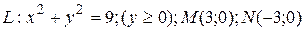 .
.
21.9 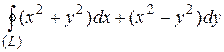 ;
; 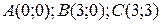 .
.
21.10 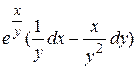 .
.
22.8 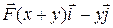 ;
; 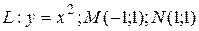 .
.
22.9 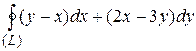 ;
; 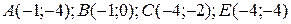 .
.
22.10 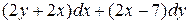 .
.
23.8 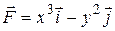 ;
; 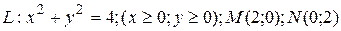 .
.
23.9 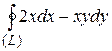 ;
; 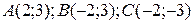 .
.
23.10 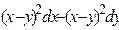 .
.
24.8 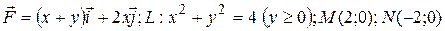 .
.
24.9 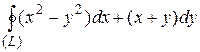 ;
; 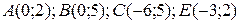 .
.
24.10 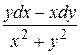 .
.
25.8 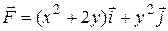 ;
; 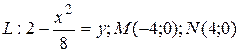 .
.
25.9 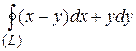 ;
; 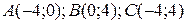 .
.
25.10 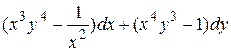 .
.
26.8 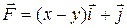 ;
; 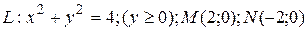 .
.
26.9 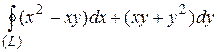 ;
; 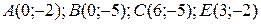 .
.
26.10 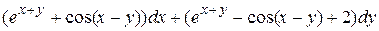 .
.
27.8 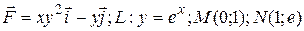 .
.
27.9 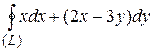 ;
; 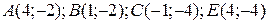 .
.
27.10 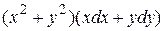 .
.
28.8 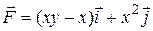 ;
; 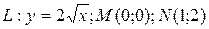 .
.
28.9 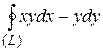 ;
; 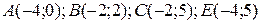 .
.
28.10 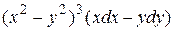 .
.
29.8 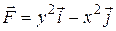 ;
; 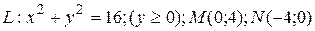 .
.
29.9 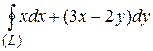 ;
; 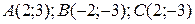 .
.
29.10 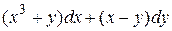 .
.
30.8 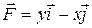 ;
; 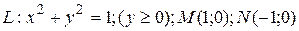 .
.
30.9 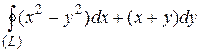 ;
; 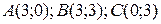 .
.
30.10 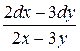 .
.
 2015-10-16
2015-10-16 255
255






