Радиусом сходимости степенного ряда 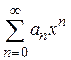 называется такое число R, при котором ряд сходится, если
называется такое число R, при котором ряд сходится, если 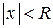 , и расходится, если
, и расходится, если 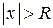 .
.
Для нахождения радиуса сходимости R составим ряд из абсолютных величин членов ряда 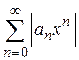 и применим признак Даламбера. Найдем
и применим признак Даламбера. Найдем
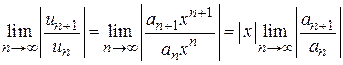 .
.
В соответствии с признаком Даламбера ряд сходится, если этот предел меньше единицы, т. е.
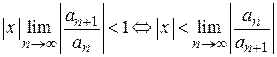 ,
,
и расходится, если 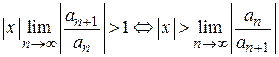 .
.
Отсюда следует, что радиус сходимости равен
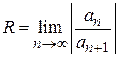 .
.
При использовании данной формулы необходимо не забывать, что в этой формуле 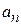 и
и 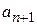 коэффициенты в членах степенного ряда при х в степени n и n +1, а не члены ряда.
коэффициенты в членах степенного ряда при х в степени n и n +1, а не члены ряда.
С помощью радиуса сходимости можно найти интервал сходимости ряда. При  степенной ряд сходится. Для того чтобы найти область сходимости, необходимо дополнительно исследовать сходимость ряда в граничных точках интервала сходимости
степенной ряд сходится. Для того чтобы найти область сходимости, необходимо дополнительно исследовать сходимость ряда в граничных точках интервала сходимости 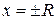 .
.
Пример 9.1. Найти область сходимости ряда 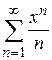 .
.
Находим радиус сходимости
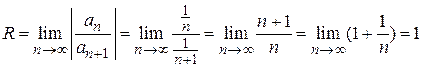 .
.
Интервал сходимости ряда 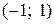 .
.
Исследуем сходимость ряда в граничных точках.
При 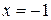 ряд имеет вид
ряд имеет вид 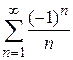 является знакочередующимся, его члены монотонно убывают и стремятся к нулю. По теореме Лейбница он сходится (см. пример 8.15).
является знакочередующимся, его члены монотонно убывают и стремятся к нулю. По теореме Лейбница он сходится (см. пример 8.15).
При  ряд
ряд 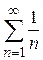 является гармоническим. Как известно он расходится.
является гармоническим. Как известно он расходится.
Следовательно, область сходимости ряда 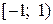 .
.
Пример 9.2. Найти область сходимости ряда 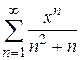 .
.
Находим радиус сходимости
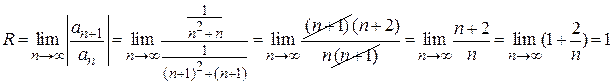 .
.
Интервал сходимости 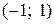 .
.
Исследуем сходимость ряда в граничных точках.
При 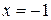 ряд имеет вид
ряд имеет вид 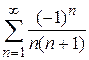 является знакочередующимся.
является знакочередующимся.
Члены ряда монотонно убывают 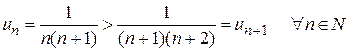
и стремятся к нулю 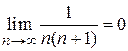 . По теореме Лейбница ряд сходится.
. По теореме Лейбница ряд сходится.
При  ряд имеет вид
ряд имеет вид  . Его сходимость исследуем по интегральному признаку Коши. Находим
. Его сходимость исследуем по интегральному признаку Коши. Находим
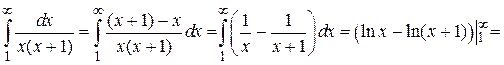
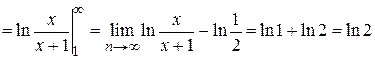 .
.
Интеграл сходится и ряд сходится.
Следовательно, область сходимости ряда 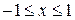 .
.
Пример 9.3. Найти область сходимости ряда 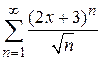 .
.
Введем новую переменную 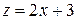 , ряд примет вид
, ряд примет вид 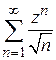 .
.
Найдем радиус сходимости этого ряда.
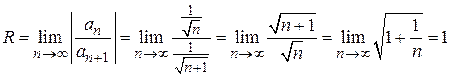 .
.
Интервал сходимости ряда 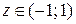 .
.
Исследуем сходимость ряда в граничных точках.
При 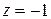 ряд имеет вид
ряд имеет вид 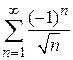 является знакочередующимся.
является знакочередующимся.
Члены ряда монотонно убывают 
и стремятся к нулю 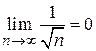 . По теореме Лейбница ряд сходится.
. По теореме Лейбница ряд сходится.
При 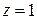 ряд имеет вид
ряд имеет вид 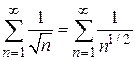 . Ряд расходится, так как степень n в знаменателе
. Ряд расходится, так как степень n в знаменателе 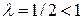 (см. пример 8.12).
(см. пример 8.12).
Область сходимости ряда 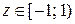 . Переходим к исходной переменной:
. Переходим к исходной переменной: 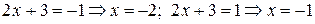
Область сходимости исходного ряда 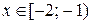 .
.
В отдельных случаях степенные ряды могут содержать только четные степени переменной 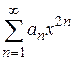 или нечетные степени
или нечетные степени 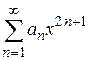 . Для нахождения радиуса сходимости ряда в таком случае составляется ряд из абсолютных величин этого ряда, а затем применяется признак Даламбера.
. Для нахождения радиуса сходимости ряда в таком случае составляется ряд из абсолютных величин этого ряда, а затем применяется признак Даламбера.
Для ряда с четными степенями 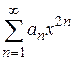 составляем ряд
составляем ряд 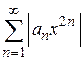 и применяем признак Даламбера
и применяем признак Даламбера 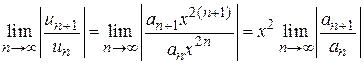 .
.
Ряд сходится, если 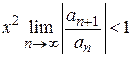 , т. е.
, т. е. 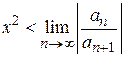 и расходится, если
и расходится, если 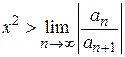 . Следовательно, можно определить квадрат радиуса сходимости такого ряда по формуле
. Следовательно, можно определить квадрат радиуса сходимости такого ряда по формуле
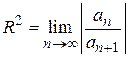 .
.
Для ряда с нечетными степенями 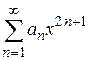 составляем ряд
составляем ряд 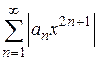 , применяем признак Даламбера
, применяем признак Даламбера 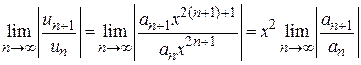 .
.
Ряд сходится, если 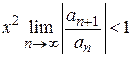 Û
Û 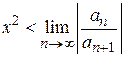 и расходится, если
и расходится, если
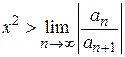 . Следовательно, в случае ряда с нечетными степенями справедлива та же формула для квадрата радиуса сходимости.
. Следовательно, в случае ряда с нечетными степенями справедлива та же формула для квадрата радиуса сходимости.
Пример 9.4. Найти область сходимости ряда 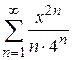 .
.
Находим 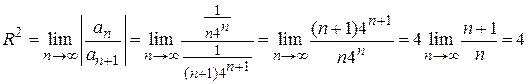 .
.
Радиус сходимости  . Интервал сходимости ряда
. Интервал сходимости ряда 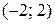 .
.
При 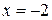
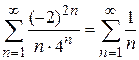 ряд расходится (гармонический).
ряд расходится (гармонический).
При 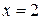
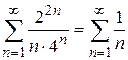 ряд расходится.
ряд расходится.
Область сходимости ряда 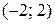 .
.
 2014-02-02
2014-02-02 124886
124886
