2015-10-16
597
ПЛАН ЛЕКЦИИ:
1. Понятие и виды средней.
2. Структурные средние: мода и медиана.
1.
Цель изучения темы: ознакомление с понятием средних величин; изучение их видов и способов расчёта.
В экономическом анализе часто приходится оперировать средними величинами в целях лучшего изучения общей картины, когда нужно из множества признаков получить 1 величину, в которой отражались бы свойства всех признаков, входящих в состав совокупности.
Каждая однородная совокупность состоит из множества единиц, которые обладают индивидуальными особенностями и отличаются друг от друга размером количественных признаков. Вместе с тем эта совокупность обладает общими типичными свойствами и чертами, выявить которые можно с помощью расчёта средних величин.
Средняя величина – обобщающий показатель, характеризующий типичный уровень варьирующего признака в расчёта на единицу совокупности.
Средняя величина – величина абстрактная, а не конкретная, так как в ней сглаживаются отклонения отдельных значений в большую или меньшую сторону. То есть средняя выражает размеры и соотношения, свойственные большинству признаков.
Существует 2 группы средних величин:
Степенные средние: средняя арифметическая, гармоническая, хронологическая, геометрическая и др.
Структурные средние: мода и медиана.
Средняя арифметическая простая рассчитывается по формуле:
,
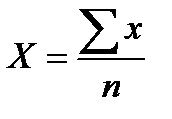где x – индивидуальные значения признака средняя которого вычисляется;
n – численность совокупности.
Эта средняя применяется в случаях, когда данные несгруппированы, то есть когда каждое индивидуальное значение признака встречается только 1 раз или одинаковое количество раз.
Если значения признаков встречаются неодинаковое количество раз то используется средняя арифметическая взвешенная:
,
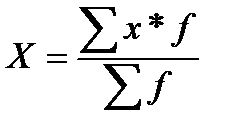где f – частота появления соответствующего значения признака.
Средняя гармоническая определяется по формулам:
Простая: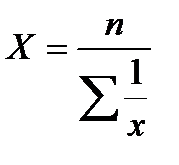 
Взвешенная: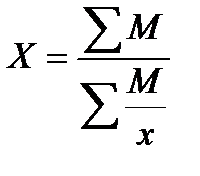 
, где М – объёмный экономический показатель.
Средняя хронологическая используется, если данные имеются на конкретные даты и вычисляется по формуле:
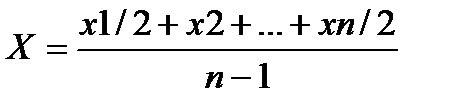
2.
Для характеристики состава совокупности применяются особые показатели, которые называются структурными средними. К ним относятся мода и медиана.
Модой в статистике называется значение признака, которое наиболее часто встречается в ряду распределения., то есть значение с наибольшей частотой.
Медианой в статистике называется значение признака, которое делит ряд распределения пополам.
В дискретном ряду формул для определения моды и медианы не требуется. В интервальном ряду мода и медиана рассчитываются по формулам:
,
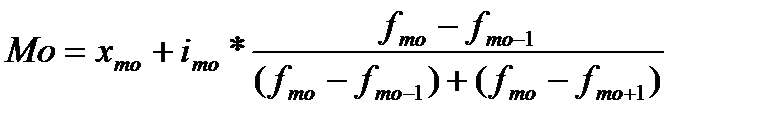где xmo – нижняя граница модального интервала;
imo – величина модального интервала;
fmo – модальная частота;
fmo-1 – частота, предшествующая модальной;
fmo+1 – частота, следующая за модальной.
,
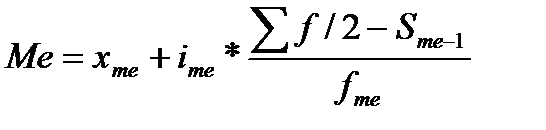где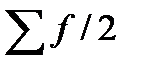 
-- полусумма всех частот;
Sme-1 – сумма накопленных частот до медианной частоты.
