ПЛАН ЛЕКЦИИ:
1. Понятие вариации признака. Абсолютные показатели вариации.
2. Относительные показатели вариации.
1.
Цель изучения: рассмотрение понятия вариации признака; изучение способов расчёта показателей вариации.
При изучении совокупности явлений нельзя ограничиваться расчётом только средних величин, так как они дают лишь обобщённую характеристику совокупности.
Изучаемые статистикой явления и процессы имеют разные значения признаков. Величины этих признаков колеблются под действием различных причин и условий. Чем разнообразнее эти причины, тем больше колеблемость (вариация).
Вариация – различие индивидуальных значений признака, которое обусловлено влиянием различных факторов.
Поскольку вариация (колеблемость) признаков может быть различной возникает необходимость измерения её величины. С этой целью в статистике используется 2 группы показателей:
Абсолютные показатели вариации;
Относительные показатели вариации.
К абсолютным показателям относятся:
Размах вариации – разность между наибольшим и наименьшим значениями признаками.
R = Xmax -- Xmin
Этот показатель имеет существенный недостаток: его величина определяется только двумя крайними значениями признака. Поэтому часто размах может неверно характеризовать колеблемость признака внутри совокупности.
Среднее линейное отклонение – средняя величина, полученная из отклонений отдельных значений признака от средней арифметической.
Для несгруппированных данных применяется следующая формула:
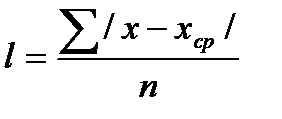
Для сгруппированных данных применяется следующая формула:

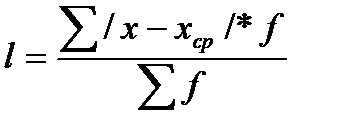
Недостаток этого показателя в том, что не учитываются знаки отклонений.
Дисперсия является основным показателем измерения колеблемости. Это средняя из квадратов отклонений отдельных значений признака от их средней арифметической.
Для несгруппированных данных применяется следующая формула:
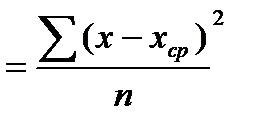
Для сгруппированных данных применяется следующая формула:
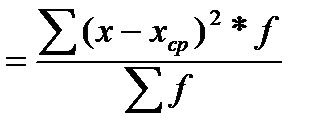
Среднее квадратическое отклонение вычисляется как корень квадратный из дисперсии.
2.
При сравнении колеблемости признаков рассчитывают относительные показатели вариации. Их вычисляют как отношение абсолютных показателей вариации к средней арифметической. Используя в качестве абсолютного показателя размах, среднее линейное отклонение или среднее квадратическое отклонение, получают следующие относительные показатели:
Коэффициент осцилляции:
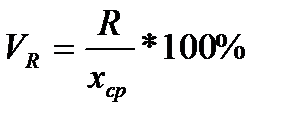
Относительное линейное отклонение:
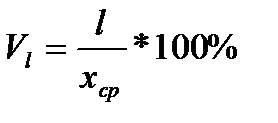
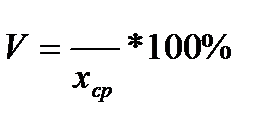
Коэффициент вариации используют для характеристики однородности совокупности. Если V не превышает 33%, то совокупность считается однородной, а средняя величина – достаточно надёжной.
 2015-10-16
2015-10-16 886
886








