Метод математической индукции является важным способом доказательства предложений (утверждений), зависящих от натурального аргумента. Метод математической индукции состоит в следующем:
Предложение (утверждение) Р(n), зависящие от натурального числа n, справедливо для любого натурального n если:
P(1) является истинным предложением (утверждением);
1. P(n) остается истинным предложением (утверждением), если n увеличить на единицу, то есть P (n+1) – истинное предложение (утверждение)
Таким образом метод математической индукции предполагают два этапа:
1. Этап проверки: проверяется, истинно ли предложение (утверждение) P (1)
2. Этап доказательства: предполагается, что предложение P (n) истинно, и доказывается истинность предложения P (n+1) (n увеличению на единицу.
Замечание 1. В некоторых случаях метод математической индукции используется в следующей форме:
Пусть m – натурально число, m > 1 и P(n) – предложение, зависящее от n, n ≥ m
Если:
1. P (m) справедливо;
2. P (n) будучи истинным предложением, влечет истинность предложения P (n+1) для любого натурального числа n, n ≥ m, тогда P (n) – истинное предложение для любого натурального n, n ≥ m.
|
|
|
В дальнейшем рассмотрим примеры применения метода математической индукции.
Пример 1. Доказать следующие равенства:
а). 1+2+3+…+n = 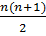
b). 1+3+5+…+ (2n-1) = 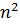
c). 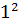 +
+ 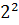 +
+ 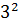 +…+
+…+ 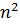 =
= 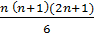
d). 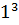 +
+ 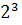 +
+ 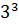 +…+
+…+ 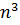 = [
= [ 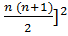
e). 1*2+2*3+3*4+…n(n+1)= 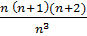
f). 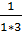 +
+ 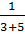 +…+
+…+ 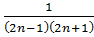 -
- 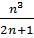
g). формула бинома Ньютона 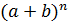 =
= 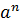 + C
+ C 
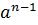 b+…+ C
b+…+ C 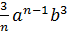 +…+ C
+…+ C 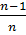
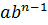 +
+ 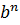 a,b є R
a,b є R
Решение. а). При n = 1 равенство примет вид 1 = 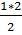 *1 = 1, следовательно, P(1) истинно. Предположим, что данное равенство справедливо, то есть, имеет место 1 + 2 +3+… n=
*1 = 1, следовательно, P(1) истинно. Предположим, что данное равенство справедливо, то есть, имеет место 1 + 2 +3+… n= 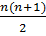 .
.
Следует проверить (доказать), что P(n+1), то есть
1+ 2 + 3 + … n + (n+1) = 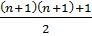 –
– 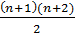
Истинно. Поскольку используется предположение индукции.
1+2+3+…+n+(n+1)- 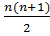 + (n+1),
+ (n+1),
Получим
1+2+3+…+ (n+1) = 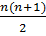 + (n+1) (
+ (n+1) ( +1) =
+1) = 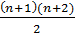
То есть, P(n+1) – истинное утверждение.
Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.
Замечание 2. Этот пример можно было решить и иначе. Действительно, сумма 1+2+3+…+n есть сумма первых n членов арифметической прогрессии с первым членом 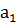 = 1 и разностью d = 1. В силу известной формулы (
= 1 и разностью d = 1. В силу известной формулы (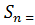
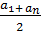 * n), то получим
* n), то получим 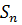 =
= 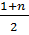 * n.
* n.
b). При n = 1 равенство примет вид: 2*1 -1 = 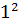 или 1 = 1, то есть Р(1) истинно. Допустим, что имеет место равенство: 1+3+5+…+(2n-1) =
или 1 = 1, то есть Р(1) истинно. Допустим, что имеет место равенство: 1+3+5+…+(2n-1) = 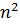
и докажем, что имеет место P(n+1):
1+3+5+…+(2n-1) +(2(n+1)-1) = 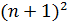
или
1+3+5+…+ (2n-1) +(2n+1) = 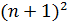
Используя предположение индукции, получим
1+3+5+…+(2n-1)+(2n+1) = 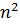 + (2n+1) =
+ (2n+1) = 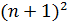
Таким образом, P(n+1) истинно и, следовательно, требуемое равенство доказано.
Замечание 3. Этот пример можно решить (аналогично предыдущему) без использования математической индукции.
17
с). При n = 1 равенство истинно: 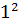 =
= 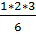 *1 = 1. Допустим, что истинно равенство
*1 = 1. Допустим, что истинно равенство 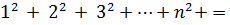
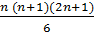
и покажем, что 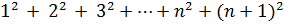 =
= 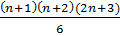
то есть истинность P (n) влечет истинность P (n+1). Действительно, 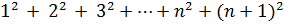 =
= 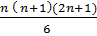 +
+ 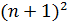 =
=
= (n+1) [ 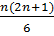 + (n+1) ] =
+ (n+1) ] = 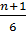 [ n(2n+1) + 6(n+1) ] =
[ n(2n+1) + 6(n+1) ] = 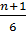 (
(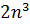 +7n+6)
+7n+6)
и, так как 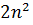 + 7n+6 = (2n+3) (n+2), получим
+ 7n+6 = (2n+3) (n+2), получим 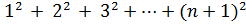 =
= 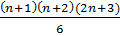
и, следовательно, исходное равенство справедливо для любого натурального n.
|
|
|
d). При n = 1 равенство справедливо: 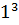 - [
- [ 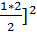 * 1 = 1. Допустим, что имеет место
* 1 = 1. Допустим, что имеет место 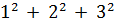 + … +
+ … + 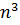 = [
= [ 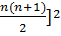
и докажем, что 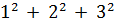 + …+
+ …+ 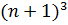 = [
= [ 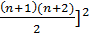
Действительно. 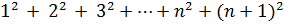 = [
= [ 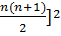 +
+ 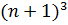 =
= 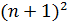 [
[ 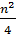 +(n+1)] =
+(n+1)] = 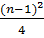 (
(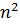 +4n+4) =
+4n+4) = 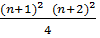 =
= 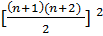
е). Утверждение Р(1) справедливо: 1*2 = 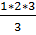 2=2. Допустим, что равенство 1*2+2*3+…+n (n+1) =
2=2. Допустим, что равенство 1*2+2*3+…+n (n+1) = 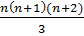
Справедливо, и докажем, что оно влечет равенство
1*2+2*3+…+n (n+1)+ (n+2) = 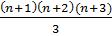
Действительно,
1*2+2*3+…+n (n+1)+ (n+1)(n+2) = 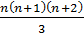 + (n+1)(n+2) = (n+1)(n+2)(
+ (n+1)(n+2) = (n+1)(n+2)( +1) =
+1) =
= 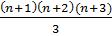
Следовательно, исходное равенство имеет место для любого натурального n.
f). P(1) справедливо: 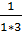 =
= 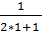 *
* 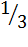 =
= 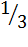 . Пусть имеет место равенство Р(n):
. Пусть имеет место равенство Р(n): 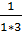 +
+ 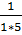 +…+
+…+ 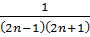 =
= 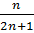
Покажем, что последние равенство влечет следующее:
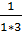 +
+ 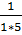 +…+
+…+ 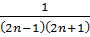 +
+ 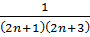 =
= 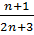
Действительно, учитывая, что P(n) имеет место, получим
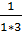 +
+ 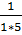 +…+
+…+ 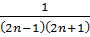 +
+ 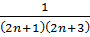 =
= 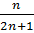 +
+ 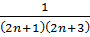 =
= 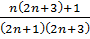 =
=
= 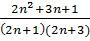 =
= 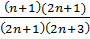 =
= 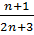
Таким образом равенство доказано.
g). При n = 1 имеем a+b+a и, следовательно, равенство справедливо.
Пусть формула бинома Ньютона справедлива при n = k, то есть 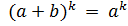 +C
+C 
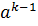 b+…+
b+…+ 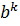
Тогда 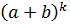 =
= 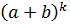 (a+b) = (
(a+b) = (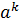 +C
+C 
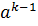 b+…+
b+…+ 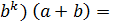
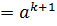 + (1+ C
+ (1+ C  )
) 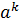 b+ (C
b+ (C 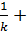 C
C  )
) 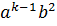 +…+ (C
+…+ (C 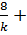 C
C 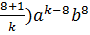 +
+
+…+ 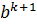
Используя равенство C 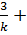 C
C 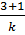 =
= 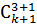 получим
получим 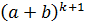 =
= 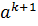 + C
+ C  +
+ 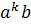 + C
+ C  +
+ 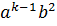 +…+
+…+ 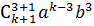 +…+
+…+ 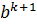
 2015-10-16
2015-10-16 11808
11808
