
Занимаясь математикой, вы постоянно пользуетесь очевидными свойствами действительных чисел, даже не замечая этого, например: сумма чисел не зависит от порядка слагаемых.
Приведем основные свойства операций сложения и умножения на множестве действительных чисел F.
1) Для каждых трех элементов a, b, c ∈ F a +(b + c)=(a + b)+ c.
2) В множестве F есть элемент 0 такой, что для каждого a ∈ F a +0=0+ a = a.
3) Для каждого элемента a ∈ F существует такой элемент x ∈ F, что a + x = x + a =0 (такой элемент называется противоположным к данному).
4) Для каждых двух элементов a, b ∈ F a + b = b + a.
5) Для каждых трех элементов a, b, c ∈ F a ∙(b ∙ c)=(a ∙ b)∙ c.
6) В множестве F есть элемент 1 (не равный 0) такой, что для каждого a ∈ F a ∙1=1∙ a = a.
7) Для каждого элемента a ∈ F, a ≠0 существует такой элемент x ∈ F, что a ∙ x = x ∙ a =1 (такой элемент называется обратным к данному).
8) Для каждых двух элементов a, b ∈ F a ∙ b = b ∙ a.
9) Для каждых трех элементов a, b, c ∈ F a ∙(b + c)= a ∙ b + a ∙ c.
Свойства 1) – 4) – это свойства операции сложения, свойства 5) – 8) – свойства операции умножения, а свойство 9) устанавливает связь между этими двумя операциями.
Оказывается, в математике существует много других множеств с парами операций на них, обладающих теми же самыми свойствами. Для таких множеств есть даже специальное название: поле.
Полем называется множество F с двумя отображениями («операциями»), каждое из которых сопоставляет любой паре элементов из F однозначно определенный третий элемент из F, и эти отображения (условно обозначаемые «+» и «∙») удовлетворяют девяти аксиомам (свойствам), приведенным выше.
Особенно важными для криптографии являются конечные поля. Сконструируем одно из таких полей.
Пусть p – простое число. Рассмотрим множество чисел {0, 1, 2,..., p −1} с операциями сложения и умножения по модулю p (суммой двух чисел считаем остаток от деления на p обычной суммы, произведением – остаток от деления на p обычного произведения). Легко проверить, что свойства 1) – 4) выполнены: для свойств 1) и 4) это очевидно, элемент 0 в свойстве 2) – это обычный нуль, противоположный к элементу a в свойстве 3) – это элемент p – a. Так же легко проверяются свойства 5), 6), 8) и 9). Свойство 7) надо доказывать. Предлагаем вам доказать это самостоятельно, поясним только идею: для каждого a ∈ {0, 1, 2,..., p −1} требуется найти такие x и y, что a x =1+ p y, т.е. a x − p y =1, а такие x и y всегда можно найти с помощью алгоритма Евклида.
Конечное поле – очень интересный математический объект. Оказывается, например, что число элементов в конечном поле может быть только степенью простого числа, и наоборот, для любого простого числа p и для любого натурального числа n существует и в некотором смысле единственное поле из p n элементов. Для него введено даже специальное обозначение: GF (p n ).
Поясним более подробно, в каком смысле поле из p n элементов единственно. В математике принято не различать многие объекты, изучаемые свойства которых совпадают. Например, для того, чтобы складывать и умножать, вовсе не обязательно учить отдельно таблицы сложения и умножения для яблок, и отдельно – для стульев. Достаточно уметь складывать числа. Число в данной ситуации можно представлять как количество единиц некоторого обобщенного продукта, неважно какого. В теории полей два поля F и G считаются «одинаковыми» или изоморфными, если можно построить такое взаимно‑однозначное отображение s: F → G, чтобы для любых x 1, x 2∈ F выполнялись условия s (x 1+ x 2)= s (x 1)+ s (x 2), s (x 1 x 2)= s (x 1) s (x 2). Фактически это означает, что можно взаимно‑однозначно сопоставить всем элементам одного поля элементы другого так, что таблицы умножения и сложения в этих полях будут «одинаковыми». Легко, например, доказать, что при изоморфизме нуль переходит в нуль, единица – в единицу.
Яркий пример использования полей в криптографии вы найдете в этюде 3.5, описывающем криптосистему RSA. Для ее полного понимания рекомендуем решить (или прочитать в любой книге по теории чисел, например, в книге И.М. Виноградова «Основы теории чисел» или в книге О. Оре «Приглашение в теорию чисел») приведенные ниже задачи.
Подумайте сами:
1. Функцией Эйлера (обозначение φ (n)) называется количество неотрицательных целых чисел, меньших n и взаимно простых с n. Пусть n = p 1α1∙...∙ p k α k, где p 1,..., p k – различные простые числа, а α 1,..., α k – натуральные. Доказать, что
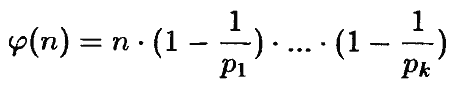
2. (Малая теорема Ферма). Пусть p – простое число, a – число взаимно простое с p. Докажите, что тогда
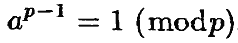
3. (Теорема Эйлера). Пусть a и n – взаимно простые числа. Докажите, что тогда
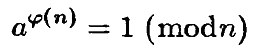
 2015-10-13
2015-10-13 458
458








