ОПРЕДЕЛЕНИЕ ЗАВИСИМОСТИ МОМЕНТА ИНЕРЦИИ СИСТЕМЫ ОТ
РАСПРЕДЕЛЕНИЯ МАССЫ ОТНОСИТЕЛЬНО ОСИ ВРАЩЕНИЯ
Методические указания к лабораторной работе № 10-Б по физике
(Раздел «Механика»)
Ростов-на-Дону 2009
Составители: С.И. Егорова, И.Н. Егоров, Г.Ф. Лемешко, В.С. Кунаков
УДК 530.1
ОПРЕДЕЛЕНИЕ ЗАВИСИМОСТИ МОМЕНТА ИНЕРЦИИ СИСТЕМЫ ОТ РАСПРЕДЕЛЕНИЯ МАССЫ ОТНОСИТЕЛЬНО ОСИ ВРАЩЕНИЯ: Метод. указания. - Ростов н/Д: Издательский центр ДГТУ, 2009. - 8 с.
Указания содержат краткое описание рабочей установки и методики определения момента инерции на приборе Обербека.
Методические указания предназначены для студентов инженерных специальностей всех форм обучения в лабораторном практикуме по физике (раздел «Механика и молекулярная физика»).
Печатается по решению методической комиссии факультета
«Нанотехнологии и композиционные материалы»
Научный редактор проф., д.т.н. В.С. Кунаков
© Издательский центр ДГТУ, 2009
ЛАБОРАТОРНАЯ РАБОТА № 10-Б
ОПРЕДЕЛЕНИЕ ЗАВИСИМОСТИ МОМЕНТА ИНЕРЦИИ СИСТЕМЫ ОТ
РАСПРЕДЕЛЕНИЯ МАССЫ ОТНОСИТЕЛЬНО ОСИ ВРАЩЕНИЯ
Цель работы: Изучение зависимости момента инерции системы от распределения массы относительно оси вращения.
Оборудование: экспериментальная установка, секундомер.
Теоретическая часть.
Маятник Обербека (рис. 1) состоит из шкива радиуса 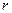 и четырёх крестообразно расположенных тонких стержней, укреплённых на одной горизонтальной оси. По стержням можно перемещать и закреплять в нужном положении четыре дополнительных груза одинаковой массы
и четырёх крестообразно расположенных тонких стержней, укреплённых на одной горизонтальной оси. По стержням можно перемещать и закреплять в нужном положении четыре дополнительных груза одинаковой массы 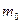 . Маятник приводится во вращательное движение при помощи груза массы
. Маятник приводится во вращательное движение при помощи груза массы 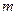 , прикреплённого к шнуру, намотанному на шкив.
, прикреплённого к шнуру, намотанному на шкив.
При разматывании нити груз 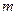 опускается, пройдя расстояние
опускается, пройдя расстояние 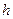 , измеряемое по шкале. Определив время падения, можно найти ускорение, с которым падает груз:
, измеряемое по шкале. Определив время падения, можно найти ускорение, с которым падает груз: 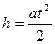
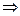
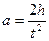 . (1)
. (1)
Запишем второй закон Ньютона для груза 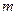 в проекции на направление движения:
в проекции на направление движения:
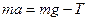
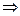
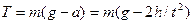 , (2)
, (2)
где 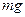 - сила тяжести,
- сила тяжести, 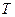 - сила натяжения нити.
- сила натяжения нити.
На шкив действует сила 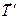 , под действием которой он совершает вращение с угловым ускорением
, под действием которой он совершает вращение с угловым ускорением
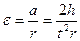 . (3)
. (3)
Поскольку по третьему закону Ньютона 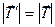 , можно записать, что момент силы, вращающий шкив, равен
, можно записать, что момент силы, вращающий шкив, равен
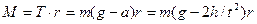 . (4)
. (4)
Запишем основное уравнение динамики вращательного движения
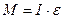
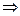
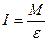 , (5)
, (5)
где 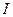 - момент инерции вращающейся системы тел маятника Обербека.
- момент инерции вращающейся системы тел маятника Обербека.
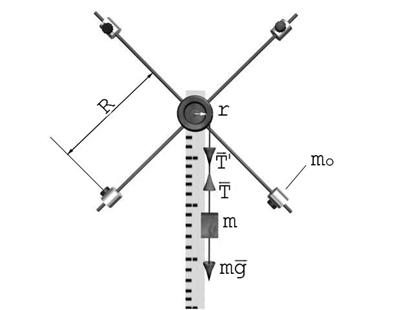
Рис. 1
Подставляя в уравнение (5) 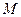 из (4) и
из (4) и 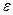 из (3), получаем
из (3), получаем
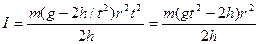 .
.
Учитывая, что радиус шкива равен половине его диаметра, т.е. 
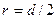 , получаем окончательную формулу для вычисления момента инерции системы:
, получаем окончательную формулу для вычисления момента инерции системы:
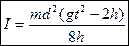 . (6)
. (6)
1. Установить на крестовине (рис. 1) симметрично четыре груза 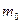 на минимальном расстоянии
на минимальном расстоянии 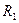 от оси вращения. Занести значение
от оси вращения. Занести значение 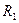 в таблицу 1.
в таблицу 1.
2. Намотать нить на шкив так, чтобы груз 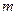 находился на определённой высоте
находился на определённой высоте 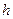 . Занести значение
. Занести значение 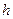 в таблицу 2.
в таблицу 2.
3. Отпустить груз и определить время падения его 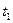 с заданной высоты. Измерения повторить несколько раз. Результаты занести в таблицу 1.
с заданной высоты. Измерения повторить несколько раз. Результаты занести в таблицу 1.
4. Занести в таблицу 2 величины, указанные на установке (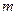 ,
, 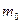 ,
, 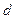 ) и их абсолютные погрешности.
) и их абсолютные погрешности.
5. Посчитать по формуле (6) момент инерции системы 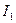 . Результат занести в таблицу 2.
. Результат занести в таблицу 2.
6. Повторить п.п. 1, 2, 3, 5 для других расстояний (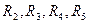 ) – по заданию преподавателя.
) – по заданию преподавателя.
7. Построить график зависимости момента инерции 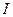 от расстояния
от расстояния 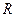 :
: 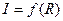 .
.
8. Произвести статистическую обработку времени 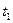 по методу Стьюдента (таблица 3).
по методу Стьюдента (таблица 3).
9. Посчитать относительную и абсолютную погрешности для 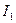 по формулам
по формулам
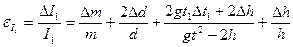 , (8)
, (8)
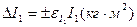 . (9)
. (9)
10. Занести значения погрешностей в таблицу 2.
Таблица 1
| №№ | 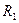 | 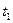 | 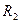 | 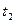 | 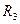 | 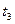 | 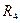 | 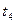 | 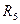 | 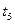 |
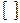 | м | с | м | с | м | с | м | с | м | с |
| Ср. |
Таблица 2
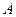 | 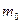 | 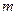 | 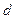 | 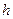 | 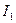 | 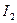 | 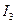 | 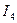 | 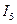 |
 | кг | кг | м | м | кг.м2 | кг.м2 | кг.м2 | кг.м2 | кг.м2 |
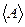 | |||||||||
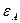 | |||||||||
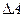 |
Таблица 3
| № пп | 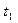 | 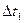 | 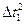 | 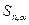 | 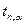 | 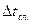 | 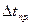 | 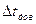 |
| с | с | с2 | с | с | с | с | ||
| Ср. |
Контрольные вопросы
1. Что называется моментом инерции материальной точки?
2. Что называется моментом инерции твёрдого тела? От чего он зависит?
3. Момент инерции тел простейшей формы относительно оси, проходящей через центр инерции.
4. Физический смысл момента инерции.
5. Что называется моментом силы?
6. Вывести рабочую формулу для определения момента инерции.
7. Записать основной закон динамики вращательного движения.
8. Теорема Штейнера.
9. Найти момент инерции однородного стержня массой 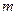 и длиной
и длиной 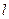 относительно оси, проходящей на расстоянии
относительно оси, проходящей на расстоянии 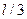 от его конца.
от его конца.
10. Вывести формулу относительной погрешности для момента инерции.
1. Савельев И.В. Курс общей физики (т.1). М.: Наука, СПб.: Лань, 2006.
2. Трофимова Т.И. Курс физики. М.: Высш. Шк., 2004.
3. Справочное руководство по физике. Ч.1. Механика, молекулярная физика, электричество, магнетизм: Учеб.-метод. пособие.-Ростов н/Д: Издательский центр ДГТУ, 2008.
 2015-10-16
2015-10-16 1005
1005








