2015-10-16
228
Маятник Максвелла являє собою диск, напресований на циліндричний стрижень. На цей диск щільно накладається кільце. Маятник Максвелла підвішується на дві нитки, які прив’язані до циліндричного стрижня і можуть намотуватися на нього.
На маятник діє сила тяжіння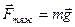 
, прикладена до його центра мас і напрямлена вниз, а також сили натягу ниток 
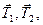напрямлені вгору. Ці сили 
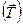створюють обертальний момент 
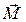відносно осі маятника 
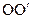(рис. 7.3). 
Під дією прикладених сил маятник здійснює складний рух, який можна розкласти на два прості: обертальний рух навколо осі 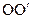та поступальний рух маятника вниз і вгору. Ці рухи маятника здійснюються при розмотуванні або намотуванні ниток підвісу.
Основний закон динаміки для поступального руху маятника матиме відповідно вигляд:
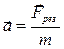, (8.1)
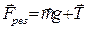
де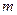 
– маса маятника, яка дорівнює сумі мас стрижня 
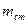, диска 
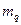і кільця 
(
); 
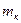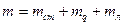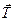– сила натягу нитки (рис. 7.3.), (
).
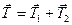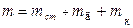
Основний закон динаміки для обертального руху буде:
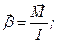(8.2)
де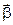 
– кутове прискорення; 
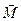– сумарний момент зовнішніх сил відносно осі 
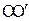, який в даному випадку дорівнює добутку сили натягу 
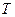на плече 
(
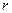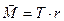); I – момент інерції маятника., відносно осі 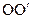складається з моментів інерції стержня Iс т, диска I д і кільця I к:
І = І ст + І д + І к (8.3)
Оскільки в обертальний рух маятник Максвела приводять (моменти) сили натягу ниток, то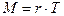 
, де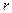 
- радіус стрижня маятника Максвела (плече сили).
Лінійне прискорення поступального руху маятника (осі 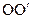) дорівнює тангенціальному прискоренню точок, які розміщуються на бічній поверхні стрижня, тобто 
.
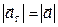У свою чергу тангенціальне прискорення пов’язане з кутовим прискоренням таким співвідношенням:
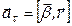(8.4)
Тоді для руху маятника вниз будуть мати в скалярній формі такий вигляд співвідношення 
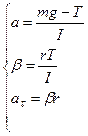(8.5)
Розв’язавши систему рівнянь (8.5) відносно значень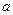 
і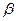 
, дістанемо:
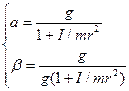(8.6)
Можна вважати, що маятник Максвелла являє собою замкнену систему тіл, сили взаємодії між якими – потенціальні (консервативні). Для такої системи справедливий закон збереження механічної енергії: повна механічна енергія замкненої системи не змінюється з часом:
W повна = W к + W п= const (8.7) Отже, під час опускання маятника його потенціальна енергія перетворюється в кінетичну енергію поступального та обертального рухів:
mgН =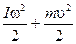 
(8.8)
де Н - відстань, на яку опустився маятник.
У нижній точці траєкторії повністю розмотана нитка починає намотуватися на стрижень у протилежному напрямку, внаслідок чого маятник піднімається вгору, а його кінетична енергія перетворюється в потенціальну. Якщо тертя відсутнє, то він підніметься до початкової висоти і кінетична енергія повністю перетвориться в потенціальну.
Якщо врахувати зв’язок між лінійною та кутовою швидкостями:
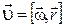; (8.9)
то для нижньої точки траєкторії співвідношенням mgh =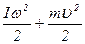 
буде мати вигляд:
mgh =(I + mr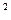 
) 
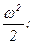(8.10)
де r – радіус циліндричного стрижня.
Кутову швидкість обертання маятника в нижній точці визначимо за часом його опускання
= 
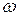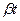(8.11)
Кутове прискорення буде
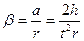(8.12)
З урахуванням цього маємо:
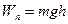(8.13)
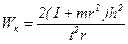(8.14)
Таким чином, за відомими параметрами маятника Максвелла (масою m, моментом інерції I, радіусом стрижня r, довжиною нитки h та часом опускання t) можна незалежно розрахувати значення кінетичної і потенціальної енергії за формулами (8.13) і (8.14) у крайніх точках траєкторії та порівняти їх.
Потрібне устаткування: Устаткування для вивчення руху маятника Максвелла; набір кілець; штангенциркуль.
