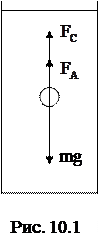
Одним из наиболее простых методов определения коэффициента динамической вязкости жидкости является метод Стокса, основанный на изучении движения тела сферической формы (шарика) в вязкой среде (рис. 10.1).
На шарик, свободно движущийся в такой среде, действуют:
Сила тяжести
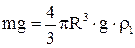 , 1.10
, 1.10
 где
где 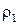 - плотность материала шарика, R – его радиус.
- плотность материала шарика, R – его радиус.
Сила Архимеда
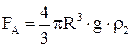 , 2.10
, 2.10
где 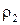 - плотность жидкости.
- плотность жидкости.
Сила сопротивления 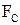 (сила внутреннего трения)
(сила внутреннего трения)
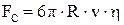 , 3.10
, 3.10
где 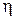 - коэффициент динамической вязкости жидкости.
- коэффициент динамической вязкости жидкости.
Следует подчеркнуть, что здесь играет роль не трение шарика о жидкость, а трение отдельных слоев жидкости друг о друга, так как при соприкосновении твердого тела с жидкостью к поверхности тела тот час же прилипают молекулы жидкости. Тело обволакивается слоем жидкости, который движется вместе с ним.
Равнодействующая этих сил
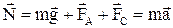 . 4.10
. 4.10
Проекция N на вертикальное направление равна
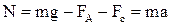 . 5.10
. 5.10
Вначале шарик будет двигаться равноускоренно, так как
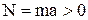 . 6.10
. 6.10
(т.е. 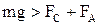 ).
).
С увеличением скорости шарика растет и сила сопротивления и наступает момент, когда равнодействующая N становится равной нулю. Это соответствует условию
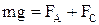 . 7.10
. 7.10
Начиная с этого момента шарик, движется равномерно с достигнутой скоростью v. Такое движение называется установившимся. При этих условиях начинает действовать закон Стокса. Для определения скорости дают шарику пройти равномерно некоторый путь h, в течение некоторого время t. Тогда
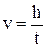 . 8.10
. 8.10
Подставляя в 8.10 выражения 1.10, 2.10, 3.10 получим
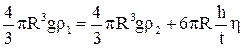 . 9.10
. 9.10
Отсюда следует, что
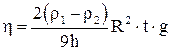 . 10.10
. 10.10
Введя обозначение
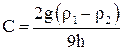 , 11.10
, 11.10
окончательно получим
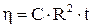 . 12.10
. 12.10
 2015-10-16
2015-10-16 682
682








