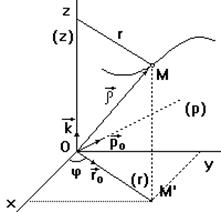
Положение точки М в пространстве определяют заданием трех ее цилиндрических координат как функций времени (рис. 20):
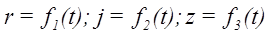
Разложение векторов скорости и ускорения на составляющие, параллельные осям цилиндрической системы координат
Or, Op, Oz выразится в следующей форме:
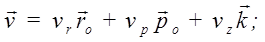
Рис. 20
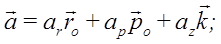
где 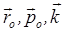 – единичные векторы, направленные по осям цилиндрической системы координат. Оси Or и Op расположены в одной плоскости с осями Ox и Oy.
– единичные векторы, направленные по осям цилиндрической системы координат. Оси Or и Op расположены в одной плоскости с осями Ox и Oy.
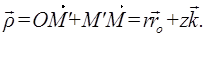 Представим радиус-вектор
Представим радиус-вектор 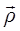 точки М как сумму двух векторов, т.е.
точки М как сумму двух векторов, т.е.
Скорость точки получим дифференцированием радиус-вектора 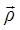 по времени:
по времени:
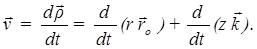
Первое слагаемое в этом выражении вычислялось при выводе скорости точки в полярных координатах. Во втором слагаемом постоянный по модулю и направлению единичный вектор 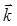 можно вынести за знак производной. В итоге для скорости получается следующее разложение на составляющие осям цилиндрической системы координат:
можно вынести за знак производной. В итоге для скорости получается следующее разложение на составляющие осям цилиндрической системы координат:
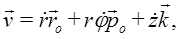
то есть, имеем, 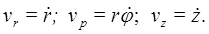 так как составляющие скорости, параллельные осям цилиндрической системы координат, взаимно перпендикулярны, то для модуля скорости имеем:
так как составляющие скорости, параллельные осям цилиндрической системы координат, взаимно перпендикулярны, то для модуля скорости имеем:
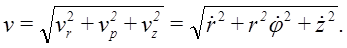
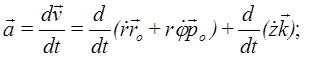 Ускорение точки получим дифференцированием по времени вектора скорости:
Ускорение точки получим дифференцированием по времени вектора скорости:
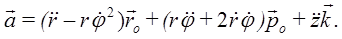
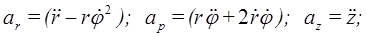 Первое слагаемое в этом выражении вычислялось при выводе ускорения в полярных координатах. Во втором слагаемом орт оси z выносим за знак производной. Получим выражение для ускорения точки в составляющих, параллельных осям цилиндрической системы координат:
Первое слагаемое в этом выражении вычислялось при выводе ускорения в полярных координатах. Во втором слагаемом орт оси z выносим за знак производной. Получим выражение для ускорения точки в составляющих, параллельных осям цилиндрической системы координат:
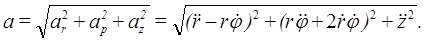
 2015-10-16
2015-10-16 334
334








