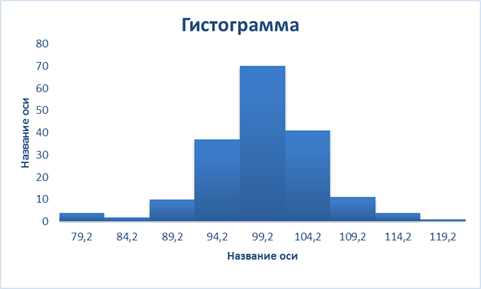
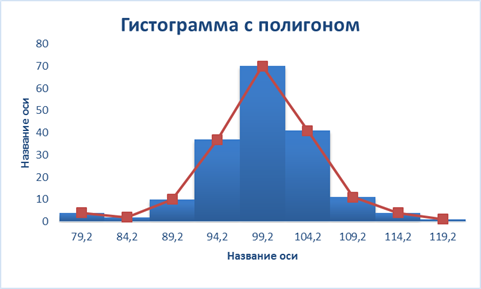
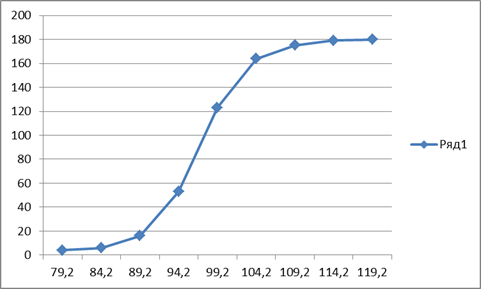
Полигон типа «больше чем…»
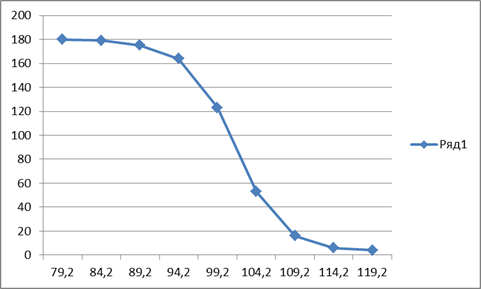
Полигон типа «меньше чем…»:
4. Сгруппированные данные:
1) Конкретное значение моды для интервального ряда рассчитывается по формуле:
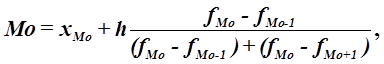
где хМo – нижняя граница модального интервала,
h –величина модального интервала,
fMo – частота модального интервала,
fMo-1 – частота интервала, предшествующего модальному,
fMo+1 – частота интервала, следующего за модальным.
Согласно таблице модальным интервалом построенного ряда является интервал 99,2 - 104,2, так как его частота максимальна и равна 70.
M0 = 99,2 + 5× 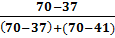 ≈ 101,8613
≈ 101,8613
Для рассматриваемой совокупности наиболее распространенное значение характеризуется средней величиной 101,8613.
2) Конкретное значение медианы для интервального ряда рассчитывается по формуле:
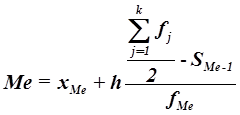 ,
,
где хМе – нижняя граница медианного интервала,
h – величина медианного интервала,
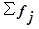 – сумма всех частот,
– сумма всех частот,
fМе – частота медианного интервала,
SMе-1 – кумулятивная (накопленная) частота интервала, предшествующего медианному.
Me = 99,2 + 5× 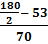 ≈ 101,843
≈ 101,843
3) Средняя арифметическая взвешенная для сгруппированных данных:
| Интервал | Частоты групп, ni | Середина интервала,
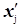
| Произведение середины интервала на частоту.
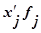 
| ||
| 79,2 – 84,2 | 81,7 | 326,8 | |||
| 84,2 –89,2 | 86,7 | 173,4 | |||
| 89,2–94,2 | 91,7 | ||||
| 94,2– 99,2 | 96,7 | 3577,9 | |||
| 99,2– 104,2 | 101,7 | ||||
| 104,2 –109,2 | 106,7 | 4374,7 | |||
| 109,2 – 114,2 | 111,7 | 1228,7 | |||
| 114,2 – 119,2 | 116,7 | 466,7 | |||
| 119,2 – 124,2 | 121,7 | 121,7 | |||
| Итого | 18305,9 | ||||
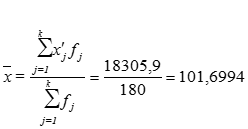
Не сгруппированные данные:
1) Для не сгруппированных данных мода будет равна 104,5, так как данное значение повторяется больше всего, чем остальные.
2) Для не сгруппированных данных медиана будет равна среднему значению 90-го и 91-го признаков: 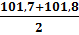 = 101,75
= 101,75
3) Для не сгруппированных данных среднюю арифметическую определим по формуле простой арифметической:
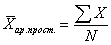 , следовательно средняя арифметическая будет равна =
, следовательно средняя арифметическая будет равна = 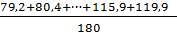 ≈ 101,52
≈ 101,52
Сравнение центральных тенденций сгруппированных и не сгруппированных данных:
1) Сравним моды сгруппированных и не сгруппированных данных:
101,8613 < 104,5 (для интервального ряда мода меньше)
2) Сравним медианы сгруппированных и не сгруппированных данных:
101,843 > 101,75 (для интервального ряда медиана будет меньше)
3) Сравним средние арифметические сгруппированных и не сгруппированных данных:
101,6994>101,52 (для интервального ряда средняя арифметическая больше)
 2015-10-16
2015-10-16 364
364







