Теоретическая часть

Аналитическая группировка – группировка, производимая с целью выявления взаимосвязи между признаками, характеризующими единицы одной статистической совокупности.

В качестве группировочного признака всегда рассматривают признак количественный, при этом являющийся фактором (условием), оказывающим влияние на формирование значений других признаков в этой совокупности, которые в этом случае принято называть результативными.

Сущность аналитической группировки состоит в том, что, разбив исходную совокупность наблюдений (единиц) на группы по значениям факторного признака (Х), вычисляют и анализируют изменение средних групповых значений результативного (зависимого) признака (Y). При наличии четко определенной тенденции в изменении этих значений судят о наличии корреляционной зависимости признака Y от фактора Х, положенного в основу группировки. Если при увеличении значений фактора Х (традиционно группировка строится по возрастанию этих значений) средние значения признака от группы к группе также увеличиваются, то делают вывод о прямой корреляционной зависимости между этими признаками. И, наоборот, если средние групповые значения признака Y уменьшаются, то говорят об обратной корреляционной зависимости между Х и Y.

Рассмотрим ряд основных правил построения аналитической группировки:

1) при небольшом объеме совокупности (не более 30 единиц) не следует образовывать большое количество групп (3-4 группы), т. к. группы могут получится малочисленными (менее 3 единиц в группе) или пустыми (ни одной единицы в группе) и обобщающие показатели, рассчитываемые в дальнейшем анализе по таким группам могут оказаться непредставительными;

2) чем больше колеблемость (вариация, изменчивость) значений группировочного признака, тем на большее количество групп следует разбивать совокупность;

3) в случае больших по объему совокупностей число групп рассчитывают по формуле Стерджесса:

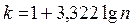, (2.1)

где n - численность совокупности (количество наблюдений, единиц совокупности).

4) после определения числа групп следует определить интервалы группировки.

Интервал – это значения варьирующего признака, лежащие в определенных границах. Каждый интервал имеет свою величину (длину, h), нижнюю (x_min) и верхнюю (x_max) границы или хотя бы одну из них.

Интервалы могут быть равные и неравные по величине.

Если вариация группировочного признака незначительна (V<33%) и распределение его значений близко к нормальному, то строят группировку с равными интервалами, где величина интервала рассчитывается по формуле

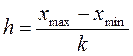, (2.2)

где x_min и x_max – соответственно минимальное и максимальное значения группировочного признака в совокупности.

Найденное значение величины интервала, будучи числом дробным, округляется всегда в бóльшую сторону с точностью:

- до десятых, если в значении величины интервала до запятой стоит один знак (например, 0,56≈0,6; 0,02≈0,1; 3,725≈3,8);

- до целого числа, если в значении величины интервала две цифры до запятой (например, 11,48≈12; 52,4≈53);

- до ближайшего целого числа, кратного 50 или 100, если в значении величины интервала до запятой стоит более чем двузначное число (например, 258≈300, 135≈150, 1227≈1250).

Первоначально аналитическая группировка строится с равными по величине интервалами. Далее анализируют распределение единиц совокупности по полученным группам, которое должно удовлетворять следующим основным требованиям:

- не должно быть пустых или малочисленных групп (т.е. количество единиц в группе должно быть не менее трех);

- ни одна из групп не должна содержать больше половины объема исходной совокупности;

- характер распределения единиц по группам должен быть близок к нормальному закону, т.е. плотность единиц в центральных группах должна быть выше, чем в крайних группах.

Если хотя бы одно из требований не выполняется, что обычно имеет место при высокой вариации значений группировочного признака, требуется перегруппировка с переходом к неравным по величине интервалам. Значения смежных границ интервалов меняются таким образом, чтобы перераспределить единицы по группам и добиться выполнимости рассмотренных требований (при этом ориентируются на значения факторного признака у единиц в каждой группе). Если при этом менялись границы первого и последнего интервалов группировки, то их делают открытыми.

Открытый интервал – интервал, у которого указана только верхняя или только нижняя его граница.

Закрытый интервал – интервал, имеющий обе свои границы.

Если в основании группировки лежит непрерывный признак, то при определении границ интервалов одно и то же значение признака выступает как нижней, так и верхней границей у двух соседних интервалов

Например,

1) до 40

2) 40 – 60

3) 60 – 80

4) 80 и свыше

Нижняя граница интервалов формируется по принципу «включительно», а верхняя граница – «исключительно».

Если в основании группировки лежит дискретный признак, то верхняя граница каждого последующего интервала больше нижней границы предыдущего интервала на единицу.

Например,

1) 40 – 60

2) 61 – 81

3) 82 – 102

Неравные интервалы могут быть прогрессивно возрастающими или убывающими, произвольными, специализированными.

Величина неравного интервала может быть найдена:

- в случае возрастания или убывания в арифметической прогрессии

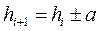, (2.3)

где а -константа;

- в случае возрастания или убывания в геометрической прогрессии

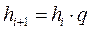, (2.4)

где q -константа (q<1 в случае убывания, q>1 в случае возрастания).

По результатам группировки вычисляются средние значения факторного и результативного признаков по каждой группе и совокупности в целом, что оформляется в виде итоговой аналитической таблицы. По характеру изменения средних групповых значений результативного признака делают вывод о том, выявлена или нет корреляционная зависимость этого признака от фактора, положенного в основу группировки, и о ее направлении (прямая или обратная). Также в выводе могут быть представлены выводы о распределении единиц по группам и дана характеристика каждой группы в отношении средних уровней изучаемых в группировке признаков в сопоставлении их значений со средними по всей совокупности.