Методические рекомендации

При выполнении задания 1 следует придерживаться следующей последовательности действий:

1) по каждому из трех признаков постройте расчетные таблицы (табл. 3.3-3.5) и выполните расчет показателей вариации;

2) рекомендации по оформлению расчетов: укажите применяемую формулу, поставьте знак равенства, выполните подстановку промежуточных результатов расчетов из соответствующей расчетной таблицы в эту формулу (обычно значения сумм из итоговой строки расчетной таблицы), поставьте знак равенства и запишите получаемое в результате значение показателя с указанием его единиц измерения;

Например,

;

;

;

.

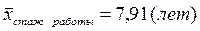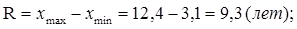
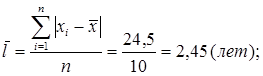
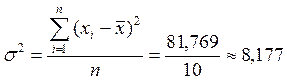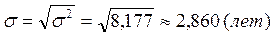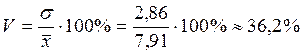3) рекомендации по округлению расчетов:

- при округлении среднего значения точность результата увеличьте на один порядок по сравнению с точностью исходных значений признака;

- при расчете показателей вариации, вычисляемых через среднее значение признака, округления результатов выполняйте с точностью увеличенной на два порядка по сравнению с точностью исходных значений признака;

- значение коэффициентов принято округлять в долях единицы - до сотых и в процентном выражении - до десятых.

Таблица 3.3 – Расчет показателей вариации значений прибыли

Номер предприятия	Прибыль, млн. руб.
…
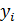
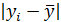
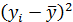
Итого

Таблица 3.4 – Расчет показателей вариации значений (название первого

факторного признака)

Номер предприятия	(Название факторного признака, единицы измерения)
…
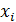
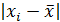
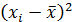
Итого

Таблица 3.5 – Расчет показателей вариации значений (название второго

факторного признака)

Номер предприятия	(Название факторного признака, единицы измерения)
…
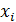
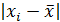
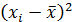
Итого

4) результаты расчета показателей по всем трем признакам сведите в одну таблицу (табл. 3.6);

5) сделайте выводы о характере и силе вариации значений каждого признака, о степени однородности совокупности предприятий в отношении каждого признака, выполните сравнительную оценку вариации признаков.

Таблица 3.6 – Показатели вариации значений признаков по совокупности предприятий розничной торговли

Показатель	Прибыль, млн. руб.   (Y)	(Название первого факторного признака, единицы измерения) (Хi)	(Название второго факторного признака, единицы измерения) (Хj)
Размах вариации
Среднее значение
Среднее линейное отклонение
Дисперсия
Среднее квадратическое отклонение
Коэффициент вариации, %

При выполнении задания 2 следует придерживаться следующей последовательности действий:

2) выпишите из итоговой аналитической таблицы (табл. 2.3), полученной в предыдущей индивидуальной работе, средние значения результативного признака Y по группам 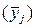и совокупности в целом (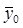), а так же значения числа наблюдений (единиц) в группах ();

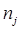3) по формуле (3.2) вычислите значение межгрупповой (факторной) дисперсии признака Y, придерживаясь рекомендаций по оформлению и округлению расчетов;

4) по формуле (3.3) вычислите значения внутригрупповых дисперсий для каждой группы, оформив промежуточные расчеты таблично (табл. 3.7, число интервалов может быть другим, в зависимости от того, как была выполнена группировка в предыдущей индивидуальной работе), придерживаясь рекомендаций по оформлению и округлению расчетов;

Таблица 3.7 – Расчет внутригрупповых дисперсий значений прибыли

Группы предприятий по (название факторного признака, единицы измерения)
(границы первого интервала)	(границы второго интервала)	(границы третьего интервала)
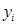
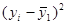
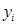
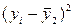
п/п			п/п			п/п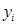
…			…			…
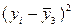
n1			n2			n3
Σ			Σ			Σ

5) вычислите по формуле (3.4) среднюю из внутригрупповых дисперсий, получив значение остаточной дисперсии признака Y, придерживаясь рекомендаций по оформлению и округлению расчетов;

6) проверьте правильность рассчитанных значений дисперсий, опираясь на правило сложения дисперсий (3.5): сумма факторной и остаточной дисперсий должна получиться равной значению общей дисперсии признака Y, полученному в задании 1;

7) сформулируйте проверяемую (нулевую) гипотезу Н₀: различия между групповыми средними значениями (название результативного признака Y) не существенны и сформировались под влиянием случайных факторов, а значит влияние (название факторного признака Х) на формирование значений (название результативного признака Y) не существенно по сравнению с влиянием этих факторов.

8) рассчитайте девиации, пользуясь формулами (3.6) и (3.7);

9) определите расчетное значение критерия Фишера и сравните его с табличным значением 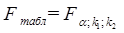(табличные значения критерия приведены в Приложении 7);

10) примите решение относительно справедливости гипотезы Н₀:

- если F_расч > F_табл, то Н₀ отвергается, а значит на 5%-ном уровне значимости можно утверждать, что влияние (название факторного признака Х) на формирование значений (название результативного признака Y) существенно по сравнению с совокупным влиянием всех прочих факторов;

- если F_расч < F_табл, то Н₀ не отвергается, а значит на 5%-ном уровне значимости можно утверждать, что влияние (название факторного признака Х) на формирование значений (название результативного признака Y) не существенно по сравнению с совокупным влиянием всех прочих факторов;

11) рассчитайте показатели: эмпирическое корреляционное отношение (η) и коэффициент детерминации (η²), сделайте по ним выводы.

Например,

.

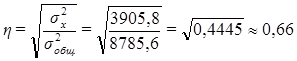Связь между стажем работы и часовой выработкой рабочего заметная.

Эмпирический коэффициент детерминации 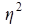= 0,445, или 44,5%.

Это означает, что 44,5% вариации часовой выработки рабочих объясняется влиянием стажа работы, и 55,5% этой вариации объясняется совокупным влияние всех других факторов.