Задание 3. Даны четыре вектора:
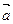 = {4;-2;- n },
= {4;-2;- n }, 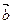 =
= 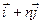 +3
+3 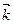 ,
, 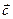 = { n;-2;-3},
= { n;-2;-3}, 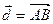 , где А (-4, 0, -8) В (4, 5, - 3); n – номер варианта. Требуется:
, где А (-4, 0, -8) В (4, 5, - 3); n – номер варианта. Требуется:
1) Найти разложение векторов 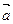 и
и 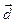 по базису векторов
по базису векторов 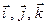 .
.
2) Найти координаты единичного вектора 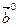 , вектора (3
, вектора (3 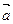 +
+ 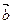 ).
).
3) Вычислить скалярное произведение векторов 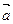 и
и 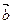 .
.
4) Найти угол между векторами 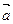 и
и 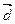 .
.
5) Найти проекцию вектора (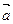 -
- 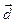 ) на вектор 2
) на вектор 2 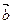 .
.
6) Найти векторное произведение векторов 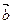 и
и 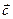 .
.
7) Найти величину угла между векторами 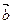 и
и 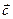 .
.
8) Проверить коллинеарность векторов 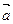 и
и 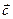 .
.
9) Проверить ортогональность векторов 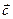 и
и 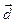 .
.
10) Найти площадь треугольника, стороны которого образуют вектора 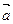 и
и 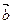 .
.
11) Проверить, образуют ли векторы 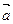 ,
, 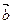 и
и 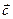 базис во множестве векторов.
базис во множестве векторов.
12) Если да, то разложить вектор 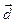 по базису векторов
по базису векторов 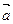 ,
, 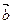 ,
, 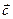 .
.
13) Проверить компланарность векторов 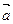 ,
, 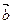 ,
, 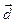 .
.
14) Найти объем параллелограмма, образованного векторами 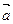 ,
, 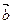 ,
, 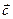 .
.
 2015-10-16
2015-10-16 215
215








