Задание №1
С помощью двойного интеграла вычислить координаты центра тяжести фигуры, ограниченной заданными линиями (поверхностную плотность считать равной единице).
1. 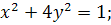
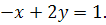
2. 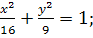
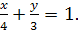
3. 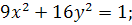
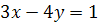 .
.
4. 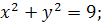
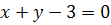 .
.
5. 
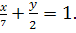
6. 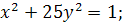
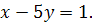
7. 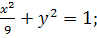
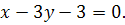
8. 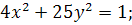
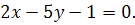
9. 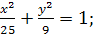
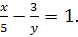
10. 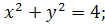
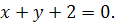
11. 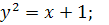
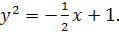
12. 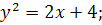
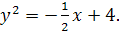
13. 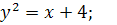
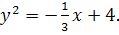
14. 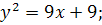
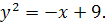
15. 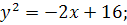
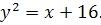
16. 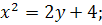
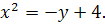
17. 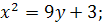
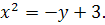
18. 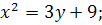
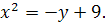
19. 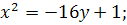
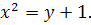
20. 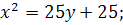
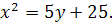
Задание № 2
Вычислить объем тела, ограниченного заданными поверхностями и расположенного в первом октанте.
1. 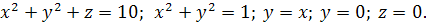
2. 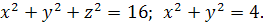
3. 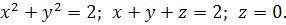
4. 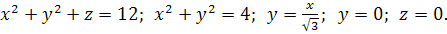
5. 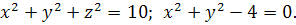
6. 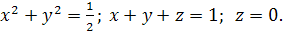
7. 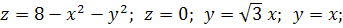
8. 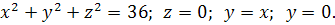
9. 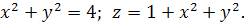
10. 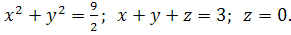
11. 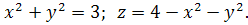
12. 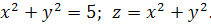
13. 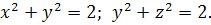
14. 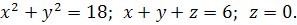
15. 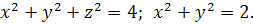
16. 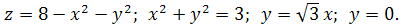
17. 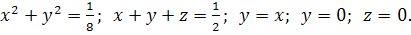
18. 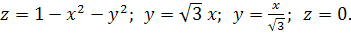
19. 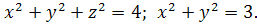
20. 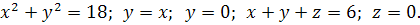
Задание №3
Вычислить работу, совершаемую переменной силой 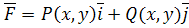 на криволинейном пути
на криволинейном пути 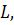 соединяющем заданные точки
соединяющем заданные точки 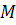 и
и 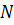 .
.
1. 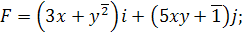
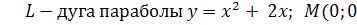 ),
), 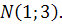
2. 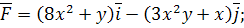
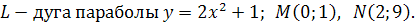
3. 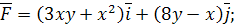
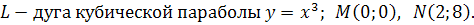
4. 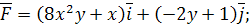
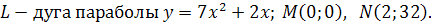
5. 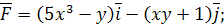
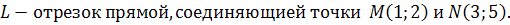
6. 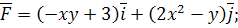
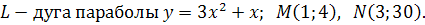
7. 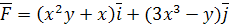 ;
;
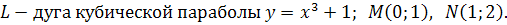
8. 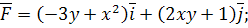
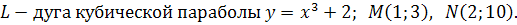
9. 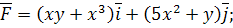
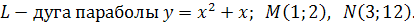
10. 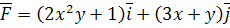
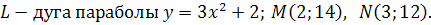
Задание № 4
Установить независимость от пути интегрирования и вычислить криволинейный интеграл по контуру, связывающему точки 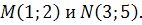
1. 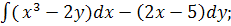
2. 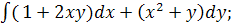
3. 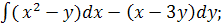
4. 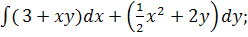
5. 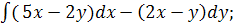
6. 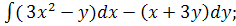
7. 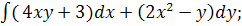
8. 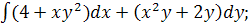
9. 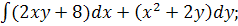
10. 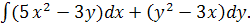
Задание 5
Найти общее решение (общий интеграл) дифференциальных уравнений первого порядка.
1. 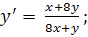
2. 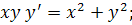
3. 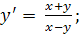
4. 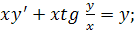
5. 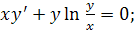
6. 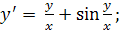
7. 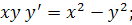
8. 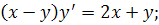
9. 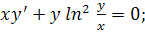
10. 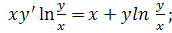
11. 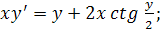
12. 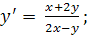
13. 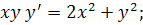
14. 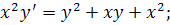
15. 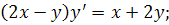
16. 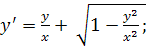
17. 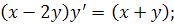
18. 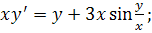
19. 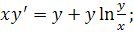
20. 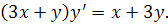
Задание № 6
Найти частное решение дифференциального уравнения, удовлетворяющее указанному начальному условию.
1. 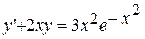 ,
, 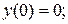
2. 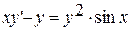 ,
, 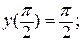
3. 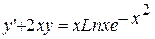 ,
, 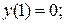
4. 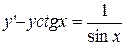 ,
, 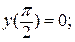
5. 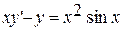 ,
, 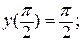
6. 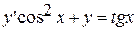 ,
, 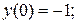
7. 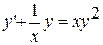 ,
, 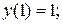
8. 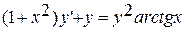 ,
, 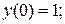
9. 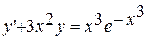 ,
, 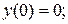
10. 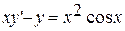 ,
, 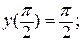
11. 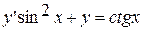 ,
, 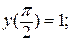
12. 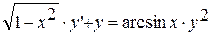 ,
, 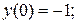
13. 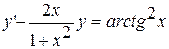 ,
, 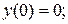
14. 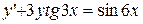 ,
, 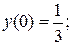
15. 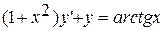 ,
, 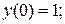
16. 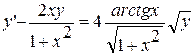 ,
, 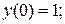
17. 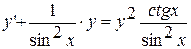 ,
, 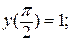
18. 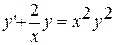 ,
, 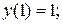
19. 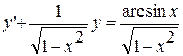 ,
, 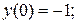
20. 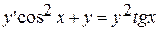 ,
, 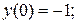
 2015-10-16
2015-10-16 242
242







