Цель работы

Научиться с помощью математического маятника, с наибольшей точностью, определять ускорение свободного падения.

1. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ.

Математическим маятником называется материальная точка, подвешенная на невесомой, нерастяжимой нити. В положении равновесия, когда маятник висит по отвесу, сила тяжести 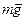уравновешивается силой натяжения нити 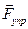.При отклонении маятника из положения равновесия на некоторый угол j появляется касательная составляющая силы тяжести F_t=-mg sinj (рис. 1). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.

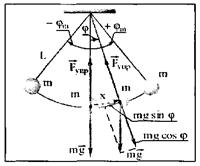
Математический маятник, j -угловое отклонение маятника от положения равновесия, х = L j -смещение маятника по дуге (Рис. 1).

Если обозначить через х линейное смещение маятника от положения равновесия по дуге окружности радиуса L, то его угловое смещение будет равно j = x / L. Второй закон Ньютона, записанный для проекций векторов ускорения и силы на направление касательной, дает:

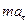= F_t = -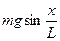

Это соотношение показывает, что математический маятник представляет собой сложную нелинейную систему, так как сила, стремящаяся вернуть маятник в положение равновесия, пропорциональна не смещению х, а .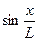

Только в случае малых колебаний, когда приближенно 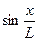можно заменить на x / L математический маятник является гармоническим осциллятром, т. е. системой, способной совершать гармонические колебания.

Практически такое приближение справедливо для углов порядка 15-20°; при этом величина 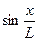отличается от x / L не более чем на 2 %.

Колебания маятника при больших амплитудах не являются гармоническими.

Для малых колебаний математического маятника второй закон Ньютона записывается в виде:

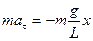
Таким образом, тангенциальное ускорение a_t маятника пропорционально его смещению х, взятому с обратным знаком. Это как раз то условие, при котором система является гармоническим осциллятором. По общему правилу для всех систем, способных совершать свободные гармонические колебания, модуль коэффициента пропорциональности между ускорением и смещением из положения равновесия равен квадрату круговой частоты:

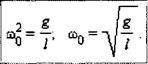
Эта формула выражает собственную частоту малых колебаний математического маятника.

Следовательно,

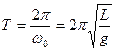
На практике приближенно в качестве математического маятника можно взять шарик, подвешенный на легкой, нерастяжимой нити. Размеры шарика должны быть малы по сравнению с длиной нити. Шарик должен быть тяжелым, тогда нить можно считать невесомой.