Приближенное вычисление функции

Постановка задачи

С точностью eps =0,001 подсчитать значение Sn функции F(x), представленной разложением в ряд S=S(x):

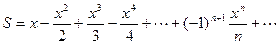
Результат сравнить со значением функции .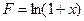

Вычисления произвести в диапазоне изменения аргумента x: 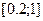с заданным шагом h=(b-a)/k, k =10. Составить программу используя операторы While и Repeat. На печать выдавать в виде таблицы: аргумент x, значения S и f, количество членов ряда n, обеспечивающих заданную точность и значения n -го члена ряда.

Изученные теоретические вопросы

Оператор повтора repeat состоит из заголовка (Repeat), тела и условия окончания (Until).

Формат оператора:

Repeat

оператор_1;

...

оператор_n;

Until условие;

Условие – выражение логического типа. Операторы, заключенные между словами Repeat и Until, являются телом цикла. Вначале выполняется тело цикла, затем проверяется условие выхода из цикла. Если результат равен False, тело цикла активизируется еще раз, если результат True – происходит выход из цикла.

Оператор Repeat имеет три характерные особенности:

· выполняется по крайней мере один раз;

· тело цикла выполняется пока условие равно False;

· в теле может находиться произвольно число операторов без операторных скобок Begin...End.

Оператор While аналогичен оператору Repeat, но проверка условия выполнения тела цикла производится в самом начале цикла.

Формат оператора:

While условие do оператор;

Условие – выражение логического типа, тело цикла – простой или составной оператор. Перед каждым выполнением оператора вычисляется значение выражения условия. Если результат условия равен True, оператор выполняется и снова вычисляется выражение условия. Если результат равен False, происходит выход из цикла и переход к первому после While оператору. Если перед первым выполнением цикла значение выражения было False, оператор вообще не выполняется и происходит переход на следующий оператор.

Операторы For, While, Repeat могут быть вложенными, т.е. в теле цикла может быть другой оператор цикла.

Приближенное вычисление функции

Функцию 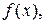n+1 раз дифференцируемую на интервале (a,b), содержащему точку с, можно разложить в ряд Тейлора, т.е. представить в виде суммы многочлена n- ой степени и остаточного члена :

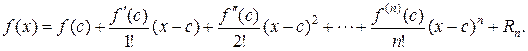
Выражение 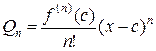называется общим членом ряда. Необходимым условием сходимости ряда является то, что общий член ряда по абсолютной величине стремится к нулю.

Вычислять значение суммы будем следующим образом: зададим начальное значение суммы, вычислим первый член суммы и добавим его к начальному значению, вычислим второй член суммы, третий и т.д., до тех пор, пока значение n -го члена суммы, по абсолютной величине, не будет меньше заданной точности 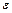(добавление его к сумме не повлияет на значение суммы). Формула общего члена ряда может принадлежать к одному из трех типов:

1) 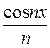; ; 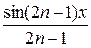;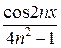... 2) ; ; ;...

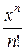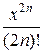3) ; ; ;...

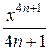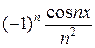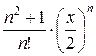В первом случае каждый член суммы вычисляется непосредственно по общей формуле. Во втором случае для вычисления суммы лучше всего использовать рекуррентные соотношения, т.е. выражать последующий член ряда через предыдущий. В последнем случае член суммы представляется в виде произведения двух сомножителей, первый из которых вычисляется с использованием рекуррентных соотношений, а второй вычисляется непосредственно.