Выражение аn определено для всех а и n, кроме случая а=0 при n≤0. Напомним свойства таких степеней.
Для любых чисел а, b и любых целых чисел m и п справедливы равенства:
am*an=am+n;
am:аn=am-n (а≠0);
(аm)n = аmn;
(ab) n = an*bn;
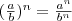 (b≠0);
(b≠0);
а1=а; а0=1 (а≠0).
Отметим также следующее свойство:
Если m>n, то аm>аn при а>1 и аm<аn при 0<а<1.
В этом пункте мы обобщим понятие степени числа, придав смысл выражениям типа 20.3, 85/7, 4-1/2 и т. д. Естественно при этом дать определение так, чтобы степени с рациональными показателями обладали теми же свойствами (или хотя бы их частью), что и степени с целым показателем. Тогда, в частности, n-я степень числа 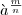 должна быть равна аm. Действительно, если свойство
должна быть равна аm. Действительно, если свойство
(ap)q=apq
выполняется, то
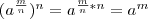
Последнее равенство означает (по определению корня n-й степени), что число 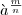 должно быть корнем п-й степени из числа аm.
должно быть корнем п-й степени из числа аm.
Определение.
Степенью числа а>0 с рациональным показателем r= 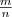 , где m — целое число, а n — натуральное (n > 1), называется число
, где m — целое число, а n — натуральное (n > 1), называется число 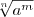
Итак, по определению
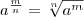 (1)
(1)
Степень числа 0 определена только для положительных показателей; по определению 0r = 0 для любого r>0.
Замечание 1.
Из определения степени с рациональным показателем сразу следует, что для любого положительного а и любого рационального r число ar положительно.
Замечание 2.
Любое рациональное число допускает различные записи его в виде дроби, поскольку 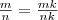 для любого натурального k. Значение ar также не зависит от формы записи рационального числа r. В самом деле, из свойств корней следует, что
для любого натурального k. Значение ar также не зависит от формы записи рационального числа r. В самом деле, из свойств корней следует, что
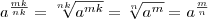
Замечание 3.
При а < 0 рациональная степень числа а не определяется, и это не случайно. Если бы мы сочли верной формулу (1) и для а<0, то, например, значение 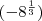 равнялось бы
равнялось бы 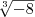 , т. е. — 2. Но, с другой стороны,
, т. е. — 2. Но, с другой стороны, 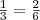 , и поэтому должно выполняться равенство
, и поэтому должно выполняться равенство 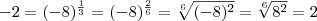 .
.
 2015-10-16
2015-10-16 5080
5080