Событие А состоит в том, что хотя бы один из 10 студентов переболел ОРЗ в осеннем семестре. Укажите событие противоположное событию а. ОРЗ

1) переболел ровно 1 студент

2) не заболел ни один студент из 10

3) переболело ровно 2 студента

4) переболело более, чем 1 студент

5) орз переболело ровно 5 студентов

6. Случайная величина распределена по нормальному закону с математическим ожиданиемM(x) = 0 и дисперсиейD(x) = 1. Определите максимальное значение функции плотности вероятности.

1) 5

2)

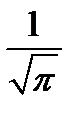
3) 0

4)

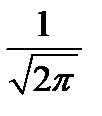
5)

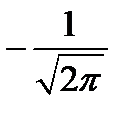
7. СЛУЧАЙНАЯ ВЕЛИЧИНА РАСПРЕДЕЛЕНА ПО НОРМАЛЬНОМУ ЗАКОНУ С МАТЕМАТИЧЕСКИМ ОЖИДАНИЕМ M(X) = 0 И СТАНДАРТНЫМ ОТКЛОНЕНИЕМ σ(x) = 1. ОПРЕДЕЛИТЕ МАКСИМАЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ ПЛОТНОСТИ ВЕРОЯТНОСТИ.

1) 5

2)

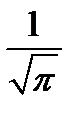
3)

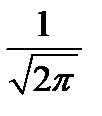
4)

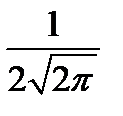
5)

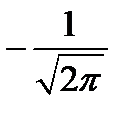
8. Одна случайная величина распределена по нормальному закону с математическим ожиданиемM(x) = 0 и стандартным отклонением σ(x) = 1, другая случайная величина распределена по нормальному закону с математическим ожиданиемM(x) = 5 истандартным отклонениемσ(x) = 2. Определите отношение максимМУМА функции плотности вероятности первой величины к максимУМУ функции плотности вероятности второй.

1) 5

2)

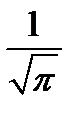
3)

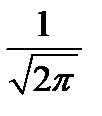
4)

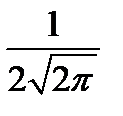
5)2

9. Одна случайная величина распределена по нормальному закону с математическим ожиданиемM(x) = 0 и дисперсиейD(x) = 1, другая случайная величина распределена по нормальному закону с математическим ожиданиемM(x) = 5 и дисперсиейD(x) = 2.Определите отношение максимМУМА функции плотности вероятности первой величины к максимУМУ функции плотности вероятности второй.

1) 5

2)

3)

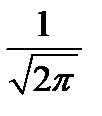
4)

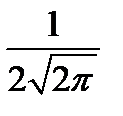
5) 2

10. Одна случайная величина распределена по нормальному закону с математическим ожиданиемM(x) = 10 и стандартным отклонением σ(x) = 1, другая случайная величина распределена по нормальному закону с математическим ожиданием M(x) = 5 и стандартным отклонением σ(x) = 1. Определите отношение максимМУМА функции плотности вероятности первой величины к максимУМУ функции плотности вероятности второй.

1) 1

2)

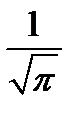
3)

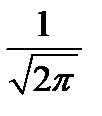
4)

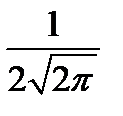
5) 2.

11. Закон распределения дискретной случайной величины задан в виде таблицы:

xi
pi	0,3	0,2	0,1	?