Методы вычислений определённых интегралов

Определённый интеграл,

Для вычисления определённых интегралов выведена формула Ньютона-Лейбница:

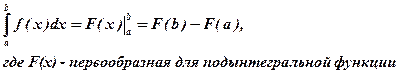
Перечислим основные свойства определённых интегралов

1.

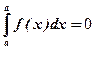
Интеграл, у которого верхний и нижний пределы интегрирования равны, равен нулю.

2.

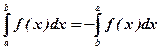
Если поменять местами пределы интегрирования, то определённый интеграл сменит знак.

3.

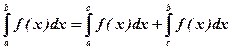
4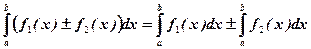

5.

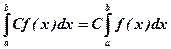
Методы вычислений определённых интегралов

1. Непосредственное интегрирование – использование формулы Ньютона-Лейбница и свойств интеграла

В этом случае вначале находят первообразную для подынтегральной функции,
далее в полученное выражение подставляют вместо аргумента верхний предел интегрирования, затем – нижний и после из первого результата вычитают второй.

Пример 1.