Линейное программирование

§ 7. Задачи линейного программирования

В предыдущих главах мы занимались только методологией исследования операций — классификацией задач, подходами к их решению и т. д., оставляя в стороне математический аппарат. В этой и последующих главах мы бегло рассмотрим некоторые из математических методов, широко применяемых в исследовании операций. В подробности этих методов не будем входить (научиться их применять по этой книжке нельзя); главное внимание обратим на их принципиальные основы.

Выше мы уже упоминали о самых простых задачах, где выбор показателя эффективности (целевой функции) W достаточно явно диктуется целевой направленностью операции, а ее условия известны заранее (де­терминированный случай). Тогда показатель эффективности зависит только от двух групп параметров: заданных условий а и элементов решения х, т. е.

W=W(a, х). (7.1)

Напомним, что в числе заданных условий а фигурируют и ограничения, налагаемые на элементы решения. Пусть решение х представляет собой совокупность п элементов решения х_і, х₂,..., х_п (иначе — n -мерный вектор):

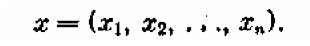
Требуется найти такие значения х_і, х ₂,..., х_п, которые обращают величину W в максимум или в минимум (оба слова в математике объединяются под одним термином «экстремум»).

Такие задачи — отыскания значений параметров, обеспечивающих экстремум функции при наличии ограничений, наложенных на аргументы, носят общее название задач математического программирования Трудности, возникающие при решении задач математического программирования, зависят: а) от вида функциональной зависимости, связывающей W с элементами решения, б) от «размерности» задачи, т. е. от количества элементов решения х₁, х₂,..., x _n, и в) от вида и количества ограничений, наложенных на элементы решения.

Среди задач математического программирования самыми простыми (и лучше всего изученными) являются так называемые задачи линейного программирования. Характерно для них то, что: а) показатель эффективности (целевая функция) W линейно зависит от элементов решения х₁, х₂,..., х_п и б) ограничения, налагаемые на элементы решения, имеют вид линейных равенств или неравенств относительно

Х1, Х2,..., Xn.

Такие задачи довольно часто встречаются на практике, например, при решении проблем, связанных с распределением ресурсов, планированием производства, организацией работы транспорта и т. д. Это и естественно, так как во многих задачах практики «расходы» и «доходы» линейно зависят от количества закупленных или утилизированных средств (например, суммарная стоимость партии товаров линейно зависит от количества закупленных единиц оплата перевозок производится пропорционально весам перевозимых грузов и т. д.).

Разумеется, нельзя считать, что все встречающиеся на практике типы зависимостей линейны; можно ограничиться более скромным утверждением, что линейные (и близкие к линейным) зависимости встречаются часто, а это уже много значит.

Приведем несколько примеров задач линейного программирования.

1. Задача о пищевом рационе. Ферма производит откорм скота с коммерческой целью. Для простоты допустим, что имеется всего четыре вида продуктов: П₁, П₂, П₃, П₄; стоимость единицы каждого продукта равна соответственно c₁, с₂, с₃, с₄. Из этих продуктов требуется составить пищевой рацион, который должен содержать: белков — не менее b₁ единиц; углеводов — не менее b ₂ единиц; жиров — не менее b ₃ единиц. Для продуктов П₁, П₂, П₃, П₄ содержание белков, углеводов и жиров (в единицах на единицу продукта) известно и приведено в таблице 7.1, где (a_іj (i = 1, 2, 3, 4; _j = 1, 2, 8) — какие-то определенные числа; первый индекс указывает номер продукта, второй — номер элемента (белки, углеводы, жиры)¹.

Таблица 7.1   Элементы Про­дукт белки угле­воды жиры П1 П2 Пз П4 а11 а21 а31 а41 а12 а22 а32 а42 а13 а23 а33 а43

Требуется составить такой пищевой рацион (т. е. назначить количества продуктов П_1? П₂, П₃, П₄, входящих в него), чтобы условия по белкам, углеводам и жирам были выполнены и при этом стоимость рациона была минимальна.

Составим математическую модель (в данном случае это очень просто). Обозначим х₁, x₂, x₃,, х₄ количества продуктов П₁, П₂, П₃, П4, входящих в рацион. Показатель эффективности, который требуется минимизировать,— стоимость рациона (обозначим ее L); она линейно

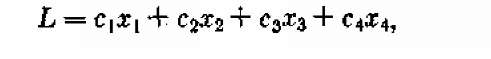
или, короче,

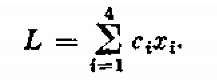(7-2)

Итак, вид целевой функции известен и она линейна. Запишем теперь в виде формул ограничительные условия по белкам, углеводам и жирам. Учитывая, что в одной единице продукта П₁ содержится а₁₁единиц белка, в х₁ единицах — а₁₁ х₁ единиц белка, в х ₂ единицах продукта П₂ содержится a ₂₁ x ₂ единиц белка и т. д., получим три неравенства:

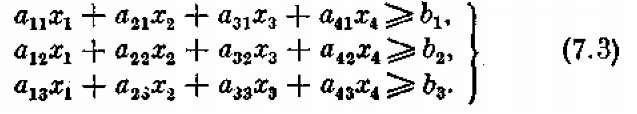
Эти линейные неравенства представляют собой ограничения, накладываемые на элементы решения х ₁, х ₂, х ₃,, х ₄.

Разумеется, мы могли бы для «оживления» материала ведать как числа b₁ b₂ b₃, так и числа a вполне конкретными значениями, но это все равно не создало бы у читателя впечатления, что автор — специалист по откорму скота.

Таким образом, поставленная задача сводится к следующей: найти такие неотрицательные значения переменных х ₁, x₂, x₃,, х₄, чтобы они удовлетворяли ограничениям — неравенствам (7.3) и одновременно обращали в минимум линейную функцию этих переменных:

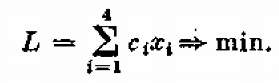
Перед нами — типичная задача линейного программирования. Не останавливаясь покуда на способах ее решения, приведем еще три примера аналогичных задач.

Таблица 72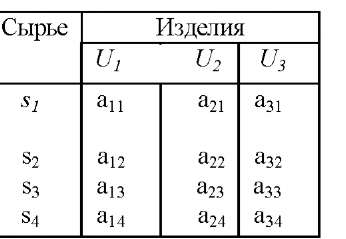

2. Задача о планировании производства. Предприятие производит изделия трех видов: U₁, U₂, U₃. По каждому виду изделия предприятию спущен план, по которому оно обязано выпустить не менее b₁ единиц изделия U₁ не менее b₂ единиц изделия U₂ и не менее b₃ единиц изделия U₃. План может быть перевыполнен, но в определенных границах; условия спроса ограничивают количества произведенных единиц каждого типа: не более соответственно β₁,β₂,β₃ единиц. На изготовление изделий идет какое-то сырье; всего имеется четыре вида сырья: s₁, s₂, s₃, s₄, причем запасы ограничены числами γ_ь γ₂, у₃, у₄ единиц каждого вида сырья. Теперь надо указать, какое количество сырья каждого вида идет на изготовление каждого вида изделий. Обозначим a_іj количество единиц сырья вида s_t (i = l, 2, 3, 4), потребное на изготовление одной единицы изделия Uj (j = 1, 2, 3). Первый индекс у числа a_ij — вид изделия, второй — вид сырья. Значения a_j сведены в таблицу (матрицу) — см. таблицу 7.2.

При реализации одно изделие U₁ приносит предприятию прибыль с₁, U₂ — прибыль с₂, U₃ — прибыль c₃- Требуется так спланировать производство (сколько каких изделий производить), чтобы план был выполнен или перевыполнен (но при отсутствии «затоваривания»), а суммарная прибыль обращалась в максимум,

Запишем задачу в форме задачи линейного программирования. Элементами решения будут х₁, x₂, x₃, — количества единиц изделий U_l, U₂, U₃, которые мы произведем. Обязательность выполнения планового задания запишется в виде трех ограничений-неравенств:

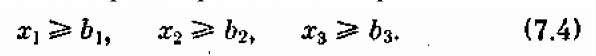
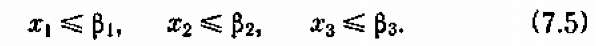
Отсутствие излишней продукции (затоваривания) даст нам еще три ограничения-неравенства:

Кроме того, нам должно хватить сырья. Соответственно четырем видам сырья будем иметь четыре ограничения-неравенства:

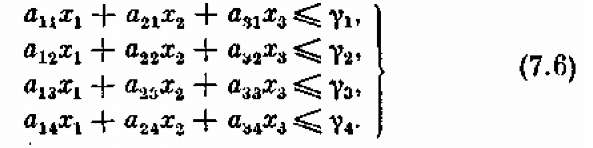
Прибыль, приносимая планом (х_і, x₂, x ₃), будет равна

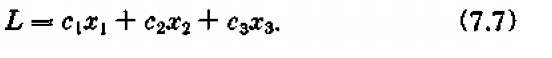
Таким образом, мы снова получили задачу линейного программирования: найти (подобрать) такие неотрицательные значения переменных х_і, x₂, x₃, чтобы они удовлетворяли неравенствам-ограничениям (7.4), (7.5), (7.6) и, вместе с тем, обращали в максимум линейную функцию этих переменных:

Задача очень похожа на предыдущую, разница в том, что неравенств-ограничений здесь больше и вместо «минимума» стоит «максимум» (а мы уже знаем, что это несущественно).

В следующей задаче мы уже встретимся с другого вида ограничениями.

3. Задача в загрузке оборудования. Ткацкая фабрика располагает двумя видами станков, из них N₁ станков типа 1 N ₂ станков типа 2. Станки могут производить три вида тканей: Т₁, T₂. Т₃, но с разной производительностью. Данные а_іj производительности станков даны в таблице 7.3 (первый индекс — тип станка, второй — вид ткани).

Таблица 13 Тип станка Вид ткани       T1 Т2 Т3   а11 а12 а13   а12 a22 a23

Каждый метр ткани вида Т₁ приносит фабрике доход с₁ вида Т₂ — доход с ₂, T ₃ — доход с ₃.

Фабрике предписан план, согласно которому она должна производить в месяц не менее b₁ метров ткани Т₁, b₂ метров ткани Т₂, b₃ метров ткани Т₃; количество метров каждого вида ткани не должно превышать соответственно β₁, β₂, β₃ метров. Кроме того, все без исключения станки должны быть загружены. Требуется так распределить загрузку станков производством тканей Т,, Т₂, T₃, чтобы суммарный месячный доход был максимален.

На первый (легкомысленный) взгляд поставленная здесь задача — родная сестра предыдущей. Рука так и тянется обозначить х,, x₂, x₃ количества тканей Т, Т₂, Тз в плане и максимизировать суммарный доход с, x, + с₂х₂ + с₃х₃. Но не торопитесь и спросите себя: а где же тут возможности оборудования? Поразмыслив, мы увидим, что в этой задаче элементы решения — не количества тканей каждого вида, а количества станков типов 1 и 2, занятых производством тканей каждого вида. Здесь удобно обозначить элементы решения буквами х с двумя индексами (первый — тип станка, второй — вид ткани). Всего будет шесть элементов решения:

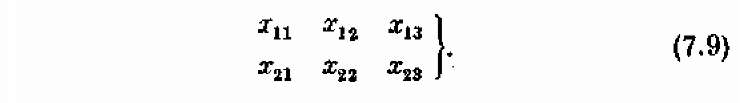
Здесь х_п — количество станков типа 1, занятых изготовлением ткани Т,, х,₂ — количество станков типа 1, занятых изготовлением ткани Т₂, и т. д.

Перед нами — еще одна задача линейного программирования. Запишем сначала условия-ограничения, наложенные на элементы решения x _ij. Прежде всего обеспечим выполнение плана. Это даст нам три неравенства- ограничения:

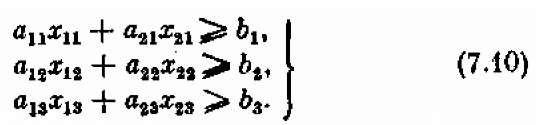
После этого ограничим перевыполнение плана; это даст нам еще три неравенства-ограничения:

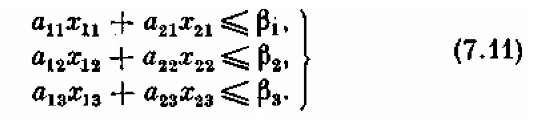
Теперь запишем ограничения, связанные с наличием оборудования и его полной загрузкой. Суммарное количество станков типа 1, занятых изготовлением всех тканей, должно быть равно N₁; типа 2 — N₂. Отсюда еще два условия — на этот раз равенства:

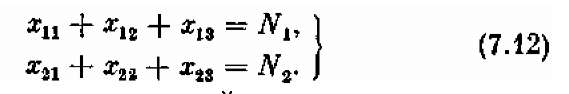
Теперь запишем суммарный доход от производства всех видов тканей. Суммарное количество метров ткани Т₁, произведенное всеми станками, будет равно a₁₁ х₁₁ + а₂₁ х₂₁ и принесет доход с₁ (а₁₁ х₁₁ + а₂₁х₂₁). Рассуждая аналогично, найдем суммарный доход фабрики за месяц при плане (7.9):

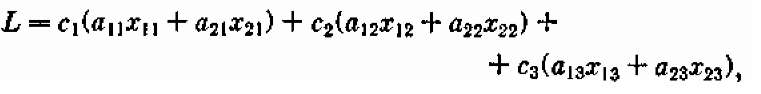
или, гораздо короче,

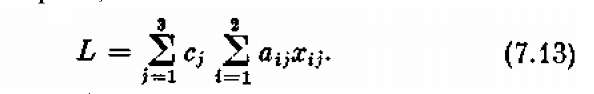
Эту линейную функцию шести аргументов мы хотим обратить в максимум: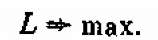

Перед нами — опять задача линейного программирования: найти такие неотрицательные значения переменных х₁₁, х₁₂,..., х₂₃, которые, во-первых, удовлетворяли бы ограничениям-неравенствам (7.10), (7.11), во- вторых — ограничениям-равенствам (7.12) и, наконец, обращали бы в максимум линейную функцию этих переменных (7.13). В этой задаче линейного про­граммирования шесть ограничений-неравенств и два ограничения-равенства.

Таблица 7.4 Предприятие База Б1 Б2 Б3 Б4 Б5 П1 Є11 Є12 с13 с,4 Є15 П2 с21 с22 с23 с24 с25 Пз сз1 с32 сзз с34 сз5

4. Задача о снабжении сырьем. Имеются три промышленных предприятия: П₁, П₂, П₃, требующих снабжения определенным видом сырья. Потребности в сырье каждого предприятия равны соответственно а ₁, a₂, a₃ единиц. Имеются пять сырьевых баз, расположенных от предприятий на каких-то расстояниях и связанных с ними путями сообщения с разными тари­фами. Единица сырья, получаемая предприятием Пі с базы Бі, обходится предприятию в c_ij рублей (первый индекс — номер предприятия, второй — номер базы, см. таблицу 7.4).

Возможности снабжения сырьем с каждой базы ограничены ее производственной мощностью: базы Б₁ Б₂, Б₃, Б₄, Б₅ могут дать не более b₁, b₂ b₃, b₄, b₅ единиц сырья. Требуется составить такой план снабжения предприятий сырьем (с какой базы, куда и какое количество сырья везти), чтобы потребности предприятий были обеспечены при минимальных расходах на сырье.

х11 х12 х13 х14 х15 х12 x22 x23 x24 x25 х13 x32 x33 x34 x35

(7.14)

Опять поставим задачу линейного программирования. Обозначим x_ij количество сырья, получаемое і-м предприятием с j -й базы. Всего план будет состоять из 15 элементов решения:

Введем ограничения по потребностям. Они состоят, в том, что каждое предприятие получит нужное ему количество сырья (ровно столько, сколько ему требуется):

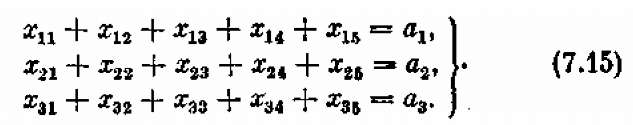
Далее напишем ограничения-неравенства, вытекающие из производственных мощностей баз:

х11+	х21+	х31≤ b1	(7.16)
х12+	х22+	х32≤ b2
х13+	х23+	х33≤ b3
х14+	х24+	х34≤ b4
х15+	х25+	х35≤ b5

Наконец, запишем суммарные расходы на сырье, которые мы хотим минимизировать. С учетом данных табл. 7.4 получим (пользуясь знаком двойной суммы):

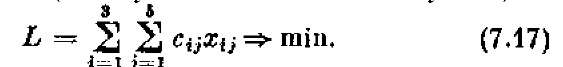
Опять перед нами задача линейного программирования: найти такие неотрицательные значения переменных х _іj, которые удовлетворяли бы ограничениям-равенствам (7.15), ограничениям-неравенствам (7.16) и обращали бы в минимум их линейную функцию (7.17).

Таким образом, мы рассмотрели несколько задач линейного программирования. Все они сходны между собой, разнятся только тем, что в одних требуется обратить линейную функцию в максимум, в других — в минимум; в одних ограничения — только неравенства, в других — как равенства, так и неравенства. Бывают задачи линейного программирования, где все ограничения — равенства. Эти различия несущественны, так как от ограничений-неравенств легко переходить к ограничениям-равенствам и обратно, как будет показано в следующем параграфе.

§ 8. Основная задача линейного программирования

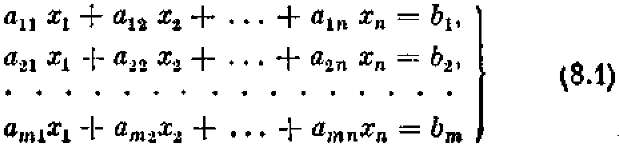
Любую задачу линейного программирования можно свести к стандартной форме, так называемой «основной задаче линейного программирования» (ОЗЛП), которая формулируется так: найти неотрицательные значения переменных х₁,х₂,..., х_п, которые удовлетворяли бы условиям-равенствам

и обращали бы в максимум линейную функцию этих переменных: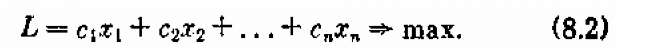

Убедимся в этом. Во-первых, случай, когда L надо обратить не в максимум, а в. минимум, легко сводится к предыдущему, если попросту изменить знак L на обратный (максимизировать не L, а V = — L). Кроме того, от любых условий-неравенств можно перейти к условиям-равенствам ценой введения некоторых новых «дополнительных» переменных. Покажем, как это делается, на конкретном примере.

Пусть требуется найти неотрицательные значения переменных х_і, x₂, х₃, удовлетворяющие ограничениям- неравенствам

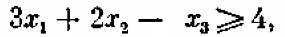(8.3)

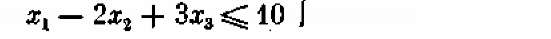(8.4)

и обращающие в максимум линейную функцию от этих переменных:

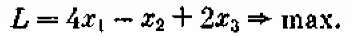(8.5)

Начнем с того, что приведем условия (8.3) к стандартной форме, так, чтобы знак неравенства был >, а справа стоял нуль. Получим:

А теперь обозначим левые части неравенств (8.5) соответственно через у_і и у₂:

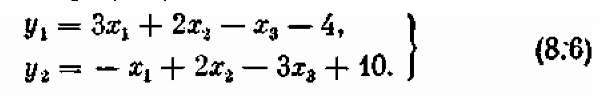
Из условий (8.5) и (8.6) видно, что новые переменные у_і и y₂ также должны быть неотрицательными.

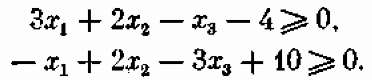
Какая же теперь перед нами стоит задача? Найти неотрицательные значения переменных x_l, x₂, x₃, y_l, y₂ такие, чтобы они удовлетворяли условиям-равенствам (8.6) и обращали в максимум линейную функцию этих переменных (то, что в L не входят дополнительные переменные у_і, у₂, неважно: можно считать, что они входят, но с нулевыми коэффициентами). Перед нами— основная задача линейного программирования (ОЗЛП). Переход к ней от первоначальной задачи с ограничениями-неравенствами (8.3) «куплен» ценой увеличения числа переменных на два (число неравенств).

Возможен и обратный переход: от ОЗЛП к задаче с ограничениями-неравенствами. Пусть перед нами основная задача линейного программирования с ограничениями-равенствами (8.1). Предположим, что среди этих т равенств линейно независимыми являются г < m¹. В линейной алгебре доказывается (см., например, [4]), что максимальное число линейно независимых равенств, связывающих п переменных х_і, x₂,..., x_n, равно п, так что вообще r < п. В линейной алгебре также доказывается, что систему из r независимых равенств с п переменными хі, х₂,..., х_п всегда можно разрешить относительно каких-то г переменных (называемых «базисными») и выразить их через остальные k = п — r переменных (называемых «свободными»). Свободным переменным можно придавать какие угодно значения, не нарушая условий (8.1). Так вот, для того чтобы перейти от условий-равенств (8.1) к условиям-неравенствам, достаточно разрешить уравнения (8.1) относительно каких-то r базисных переменных, выразить их через свободные, а затем вспомнить, что все переменные должны быть неотрицательными, и записать условия их неотрицательности в виде ограничений-неравенств. А потом «забыть» о базисных переменных и манипулировать только свободными, число которых будет k = п — r. При этом надо будет освободить от базисных переменных также и функцию L, подставив в нее их выражения через свободные. Таким образом, при переходе от ОЗЛП к задаче с ограничениями- неравенствами число переменных не увеличивается, а уменьшается на число r независимых условий-равенств в ОЗЛП. Примеров такого перехода мы приводить не будем, предоставляя пытливому читателю самому убедиться в его возможности.

Итак, всякая задача линейного программирования может быть сведена к стандартной форме ОЗЛП. Мы не будем подробно останавливаться на способах решения этой задачи. Им посвящены специальные руководства (например, [4, 5]), они описаны во многих книгах по исследованию операций (например, [6, 7]). В следующем параграфе мы изложим только некоторые соображения общего характера относительно существования решения ОЗЛП и способов его нахождения. Никакими расчетными алгоритмами мы заниматься не будем, а отошлем интересующегося читателя к вышеупомянутым руководствам.

§ 9. Существование решения ОЗЛП и способы его нахождения

Рассмотрим основную задачу линейного программирования (ОЗЛП): найти неотрицательные значения переменных х₁, х₂,..., х_п, удовлетворяющие т условиям- равенствам:

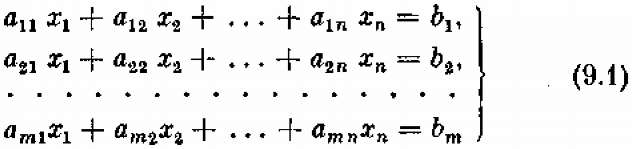
и обращающие в максимум линейную функцию этих переменных:

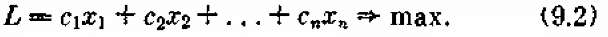
Для простоты предположим, что все условия (9.1) линейно независимы (r = т), и будем вести рассуждения в этом предположении.

Назовем допустимым решением ОЗЛП всякую совокупность неотрицательных значений x_l, х₂,..., х_п, удовлетворяющую условиям (9.1). Оптимальным назовем то из допустимых решений, которое обращает в максимум функцию (9.2). Требуется найти оптимальное решение.

Всегда ли эта задача имеет решение? Нет, не всегда. Во-первых, может оказаться, что уравнения (9.1) вообще несовместны (противоречат друг другу). Может оказаться и так, что они совместны, но не в области неотрицательных решений, т. е. не существует ни одной совокупности чисел x_l >0, x₂ >0,..., x_ri >0, удовлетворяющей условиям (9.1). Наконец, может быть и так, что допустимые решения ОЗЛП существуют, но среди них нет оптимального: функция L в области допустимых решений не ограничена сверху. Все эти опасности подстерегают нас, главным образом, в «придуманных», искусственно поставленных задачах, хотя иногда легкомысленное планирование (неполный учет имеющихся ресурсов) приводит к неразрешимым задачам линейного программирования.

Чтобы представить себе принципиальную сторону ОЗЛП, обратимся к геометрической интерпретации. Пусть число уравнений т на два меньше числа переменных п (п — т = к = 2). Такой частный случай дает возможность геометрической интерпретации ОЗЛП на плоскости.

Мы знаем, что т линейно независимых уравнений (9.1) всегда можно разрешить относительно каких-то т базисных переменных, выразив их через остальные, свободные, число которых равно га — т = к (в нашем случае к = 2). Предположим, что свободные переменные— это x_l и x₂ (если это не так, то всегда можно заново перенумеровать переменные), а остальные: х₃, Х4,..., хп — базисные. Тогда вместо т уравнений (9.1) мы получим тоже т уравнений, но записанных в другой форме, разрешённых относительно х₃, x₄,...:

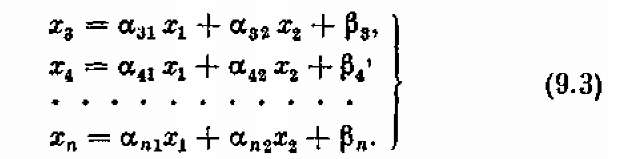
Будем изображать пару значений свободных переменных точкой с координатами х_і, х₂ (рис. 9.1). Так как переменные х_і, х₂ должны быть неотрицательными, то допустимые значения свободных переменных лежат только выше оси Ох_і (на которой х₂ = 0) и правее оси Ox₂ (на которой х_і = 0). Это мы отметим штриховкой, обозначающей «допустимую» сторону каждой оси.

Теперь построим на плоскости x₁ Ox₂ область допустимых решений или же убедимся, что ее не существует. Базисные переменные х₃, х₄,..., х_п тоже должны быть неотрицательными и удовлетворять уравнениям (9.3). Каждое такое уравнение ограничивает область допустимых решений. Действительно, положим в первом уравнении (9.3) х₃ = 0; получим уравнение прямой линии:

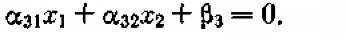
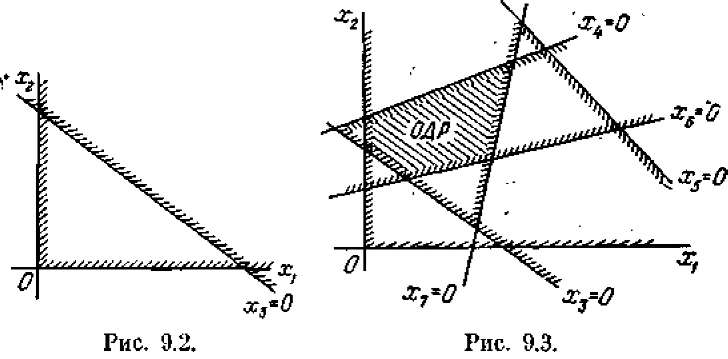
На этой прямой х₃ = 0; по одну сторону от нее х₃ > 0, по другую — х₃ < 0. Отметим штриховкой ту сторону (полуплоскость), где х₃ > 0 (рис. 9.2). Пусть эта сторона оказалась правее и выше прямой х₃ = 0. Значит, вся область допустимых решений (ОДР) лежит в первом координатном угле, правее и выше прямой х₃ = 0. Аналогично поступим и со всеми остальными условиями (9.3). Каждое из них изобразится прямой со штриховкой, указывающей «допустимую» полуплоскость, где только и может лежать решение (рис. 9.3).

Рис, 9.4.

Таким образом, мы построили п прямых: две оси координат (Ох₁ и Ох₂) и п — 2 прямых х₃ = 0, х₄ = 0,..., х_п = 0. Каждая из них определяет «допустимую» полуплоскость, где может лежать решение. Часть первого координатного угла, принадлежащая одновременно всем этим полуплоскостям, и есть ОДР. На рис. 9.3 показан случай, когда ОДР существует, т. е. система уравнений (9.3) имеет неотрицательные решения. Заметим, что этих решений— бесконечное множество, так как любая пара значений свободных переменных, взятая из ОДР, «годится», а из х₁ и х₂ могут быть определены и базисные переменные. Может оказаться, что область допустимых решений не существует, и значит, уравнения (9.3) несовместны в области неотрицательных значений. Такой случай показан на рис. 9.4, где нет области, лежащей одному сторону от всех прямых. Значит, ОЗЛП не имеет решения.

Предположим, что область допустимых решений существует, и мы ее построили. Как же теперь найти среди них оптимальное?

Для этого дадим геометрическую интерпретацию условию (9.2) L=>max. Подставив выражения (9.3) в формулу (9.2), выразим L через свободные переменные х₁, х₂. После приведения подобных членов получим:

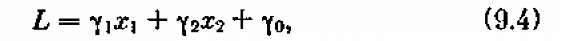
где γ₁, γ₂ — какие-то коэффициенты, γ ₀ — свободный член, которого в первоначальном виде у функции L не было; теперь, при переходе к переменным х₁, х₂, он мог и появиться. Однако мы его тут же и отбросим: ведь максимум линейной функции L достигается при тех же значениях х₁, х₂, что и максимум линейной однородной функции (без свободного члена):

Посмотрим, как изобразить геометрически условие L' => max. Положим сначала L = 0, т. е. γ ₁ x₁ + γ ₂ x₂ = 0, и построим на плоскости x_lОх₂ прямую с таким уравнением; очевидно, она проходит через начало координат (рис. 9.5). Назовем ее «опорной прямой». Если мы будем придавать L какие-то значения C_l, С₂, С₃,.., прямая будет перемещаться параллельно самой себе; при перемещении в одну сторону L′ будет возрастать, в другую — убывать. Отметим на рис. 9.5 стрелками, поставленными у опорной прямой, то направление, в котором возрастает. На рис. 9.5 это оказалось направление «направо — вверх», но могло быть и наоборот: все зависит от коэффициентов γ₁, γ ₂. Теперь изобразим опорную прямую и ОДР на одном чертеже (рис. 9.6). Давайте будем мысленно двигать опорную прямую параллельно самой себе в направлении стрелок (возрастания L ′). Когда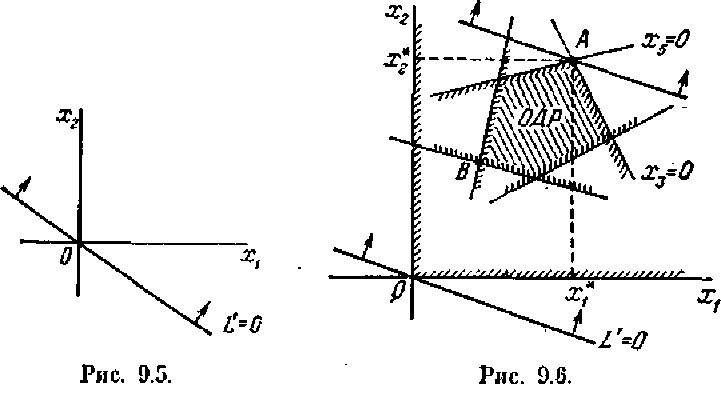

L′ достигнет максимума? Очевидно, в точке А (крайней точке ОДР в направлении стрелок). В этой точке свободные переменные принимают оптимальные значения x₁*, х₂*, а из них можно по формулам (9.3) найти и оптимальные значения всех остальных (базисных) переменных x₃*, x₄*,..., x_п^*1 Заметим, что максимум LL достигается в одной из вершин ОДР, где по крайней мере две из базисных переменных (в нашем случае это х ₃ и х₅) обращаются в нуль. Могло бы обращаться в нуль и больше базисных переменных, если бы через точку А проходило более двух прямых х_і = 0.

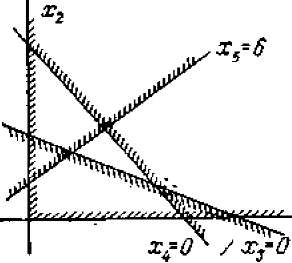
А может ли оказаться, что оптимального решения не существует? Да, может, если в ОДР функция L' (а значит и L) не ограничена сверху. Пример такого ненормального случая показан на рис. 9.7 (в разумно поставленных задачах обычно такого недоразумения не возникает).

На рис. 9.6 оптимальное решение существовало и было единственным. А сейчас рассмотрим случай, когда оптимальное решение существует, но не единственно (их бесконечное множество). Это случай, когда максимум L' достигается не в одной точке А, а на целом отрезке АВ, параллельном опорной прямой (рис. 9.8). Такой случай встречается на практике, но нас он

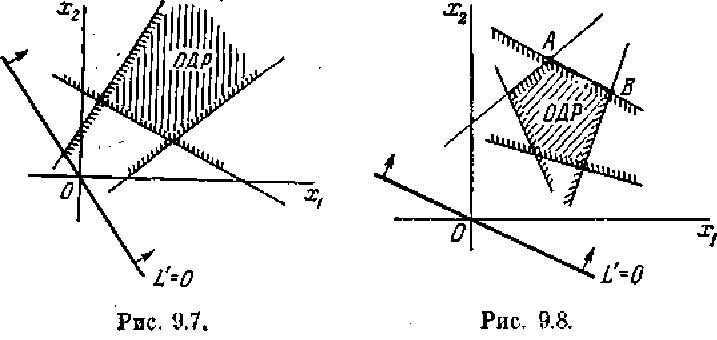
не должен волновать. Все равно и в этом случае максимум L' достигается в какой - то из вершин ОДР (А или В — безразлично), и в поисках оптимального решения можно ограничиться вершинами ОДР.

¹Если бы стрелки были направлены иначе («налево — вниз»), то крайней точкой ОДР в направлении стрелок была бы точка В.

Итак, мы рассмотрели в геометрической интерпретации случай п — т = k =2 и убедились в следующем: оптимальное решение (если оно существует) всегда достигается в одной из вершин ОДР, в точке, где по крайней мере две из переменных х₁, х₂,..., х_п равны нулю.

Оказывается, аналогичное правило справедливо и в случае n — m = k>2 (только геометрическая интерпретация теряет в этом случае свою наглядность). Обойдемся без доказательства, просто сформулируем это правило.

Оптимальное решение ОЗЛП (если оно существует) достигается при такой совокупности значений переменных х₁, х₂,..., х_п, где по крайней мере к из них обращаются в нуль, а остальные неотрицательны.

При k = 2 такая совокупность значений изображается точкой на плоскости, лежащей в одной из вершин многоугольника допустимых решений (ОДР). При k = 3 ОДР представляет собой уже не многоугольник, а многогранник, и оптимальное решение достигается в одной из его вершин. При k > 3 геометрическая интерпретация теряет наглядность, но все же геометрическая терминология остается удобной. Мы будем продолжать говорить о «многограннике допустимых решений» в k-мерном пространстве, а оптимальное решение (если оно существует) будет достигаться в одной из вершин этого многогранника, где по крайней мере к переменных равны нулю, а остальные — неотрицательны. Будем для краткости называть такую вершину «опорной точкой», а вытекающее из нее решение — «опорным решением».

Отсюда вытекает идея, лежащая в основе большинства рабочих методов решения ОЗЛП,— идея «последовательных проб». Действительно, попробуем разрешить уравнения (9.1) относительно каких-нибудь т базисных переменных и выразим их через остальные к свободных. Попробуем положить эти свободные переменные равными нулю — авось повезет, наткнемся на опорную точку. Вычислим базисные переменные при нулевых значениях свободных. Если все они оказались неотрицательными, значит, нам повезло, мы сразу же получим допустимое (опорное) решение, и его остается только оптимизировать. А если нет? Значит, данный выбор свободных и базисных переменных допустимого решения не дает; точка лежит не на границе, а вне ОДР. Что делать? Надо «переразрешить» уравнения относительно каких-то других базисных переменных, но не как попало, а так, чтобы это приближало нас к области допустимых решений (для этого в линейном программировании существуют специальные приемы, на которых мы останавливаться не будем). Пусть, наконец, несколько раз повторив такую процедуру, мы нашли опорное решение ОЗЛП. Браво! Но это еще не все. Тут надо поставить вопрос: а является ли это решение оптимальным? Выразим функцию L через последние получившиеся свободные переменные и попробуем увеличивать их сверх нуля. Если от этого значение L только уменьшается, значит, нам повезло, и мы нашли оптимальное решение, ОЗЛП решена. А если нет? Снова «переразрешаем» систему уравнений относительно других базисных переменных, и снова не как попало, а так, чтобы, не выходя за пределы допустимых решений, приблизиться к оптимальному. И опять-таки для этого в линейном программировании существуют специальные приемы, гарантирующие, что при каждом новом «переразрешении» мы будем приближаться к оптимальному решению, а не удаляться от него. На этих приемах мы тоже здесь не будем останавливаться. После конечного числа таких шагов цель будет достигнута — оптимальное решение найдено. А если его не существует? Алгоритм решения ОЗЛП сам покажет вам, что решения нет.

Читатель, может быть, спросит: только-то и всего? Зачем было придумывать хитрые методы решения ОЗЛП, может быть, надо просто перебрать, одну за другой, все возможные комбинации к свободных пере­менных, полагая их равными нулю, пока, наконец, не будет найдено оптимальное решение?

Действительно, для простых задач, где число переменных невелико, такой «слепой перебор» может привести к решению, и довольно быстро. Но на прак­тике часто встречаются задачи, в которых число переменных (и наложенных условий) очень велико, порядка сотен и даже тысяч. Для таких задач простой перебор становится практически невозможным: слишком велико число комбинаций свободных и базисных переменных. Пример: только при п = 30 и т = 10 число возможных комбинаций свободных переменных с базисными равно С₃₀¹⁰ = 30 045 015, т. е. свыше 30 миллионов! А эта задача — далеко не из сложных.

Разработанные в теории линейного программирования вычислительные методы («симплекс-метод», «двойственный симплекс-метод» и другие, см. [4, 6, 8]) позволяют находить оптимальное решение не «слепым» перебором, а «целенаправленным», с постоянным приближением к решению. Добавим, что современные ЭВМ, как правило, снабжены подпрограммами для решения задач линейного программирования, так что лицу, желающему их решать, нет даже особой надобности обучаться решению таких задач «вручную» — труд крайне неприятный и изнурительный.