Какое значение приняла случайная величина X?

Если случайная величина X дискретна, т. е. имеет значения x₁, x₂,..., х_к с вероятностями р₁, р₂,..., р_к то, очевидно, случай сводится к предыдущему. Теперь рассмотрим случай, когда случайная величина непрерывна и имеет заданную плотность вероятности f(x). Чтобы разыграть ее значение, достаточно осуществить следующую процедуру: перейти от плотности вероятности f(x) к функция распределения F(x) по формуле

х

F(x) = ∫ f(х) dx, (23.1)

-∞

затем найти для функции F обратную ей функцию Ψ. Затем разыграть случайное число R от 0 до 1 и взять от него эту обратную функцию:

Х =Ψ (R) (23.2)

Можно доказать (мы этого делать не будем), что полученное значение X имеет как раз нужное нам распределение. f(x).

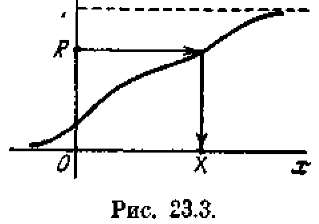
Графически процедура розыгрыша значения X показана на рис. 23.3. Разыгрывается число R от 0 до 1 и для него ищется такое значение X, при котором F(X) = R (это показано стрелками на рис. 23.3).

На практике часто приходится разыгрывать значение случайной величины, имеющей нормальное распределение. Для нее, как для любой непрерывной случайной величины, правило розыгрыша (23.2) остается справедливым, но можно поступать и иначе (проще). Известно, что (согласно центральной предельной теореме теории вероятностей) при сложении достаточно большого числа независимых случайных величин с одинаковыми распределениями получается случайная величина, имеющая приближенно нормальное распределение. На практике, чтобы получить нормальное распределение, достаточно сложить шесть экземпляров случайного числа от 0 до 1. Сумма этих шести чисел

Z = R₁+ R₂ +…R₆ (28.3)

имеет распределение, настолько близкое к нормальному, что в большинстве практических задач им можно заменить нормальное. Для того чтобы математическое ожидание и среднее квадратическое отклонение этого нормального распределения были равны заданным m_x, σ_x, нужно подвергнуть величину Z линейному преобра­зованию и вычислить

X = σ_х √2 (Z - 3) + т_х. (23.4)

Это и будет нужная нам нормально распределенная случайная величина.

4. Какую совокупность значений приняли случайные величины X₁,X₂,...,X_k? Если случайные величины независимы, то достаточно k раз повторить процедуру, описанную в предыдущем пункте. Если же они зави­симы, то разыгрывать каждую последующую нужно на основе ее условного закона распределения при условии, что все предыдущие приняли те значения, которые дал розыгрыш (более подробно останавливаться на этом случае мы не будем).

Таким образом, мы рассмотрели все четыре варианта единичного жребия и убедились, что все они сводятся к розыгрышу (одно- или многократному) случайного числа R от 0 до 1.

Возникает вопрос: а как же разыгрывается это число R? Существует целый ряд разновидностей так называемых «датчиков случайных чисел», решающих эту задачу. Остановимся вкратце на некоторых из них.

Самый простой из датчиков случайных чисел — это вращающийся барабан, в котором перемешиваются перенумерованные шарики (или жетоны). Пусть, например, нам надо разыграть случайное число R от 0 до 1 с точностью до 0,001. Заложим в барабан 1000 перенумерованных шариков, приведем его во вращение и после остановки выберем первый попавшийся шарик, прочтем его номер и разделим на 1000.

Можно поступить и немного иначе: вместо 1000 шариков заложить в барабан только 10, с цифрами 0, 1, 2,..., 9. Вынув один шарик, прочтем первый десятичный знак дроби. Вернем его обратно, снова покрутим барабан и возьмем второй шарик — это будет второй десятичный знак и т. д. Легко доказать (мы этого делать не будем), что полученная таким образом десятичная дробь будет иметь равномерное распределение от 0 до 1. Преимущество этого способа в том, что он никак не связан с числом знаков, с которым мы хотим знать R.

Отсюда один шаг до рационализаторского предложения: не разыгрывать число R каждый раз, когда это понадобится, а сделать это заранее, т. е. составить достаточно обширную таблицу, в которой все цифры 0, 1, 2,.... 9 встречаются случайным образом и с одинаковой вероятностью (частотой). До этого приема люцесса, что и множество реализаций той же общей продолжительности.

Пусть в нашем распоряжении — одна длинная реализация стационарного случайного процесса общей продолжительности Т. Тогда интересующие нас вероятности состояний можно найти, как долю времени, которую система проводит в этих состояниях, а средние значения случайных величин получить усреднением не по множеству реализаций, а по времени, вдоль реализации.

Рассмотрим пример. Моделируется методом Монте-Карло работа немарковской одноканальной СМО с очередью: Число мест в очереди ограничено двумя. Заявка, пришедшая в момент, когда оба места в очереди заняты, покидает СМО необслуженной (получает отказ). Время от времени канал может выходить из строя. Если канал вышел из строя, находившиеся в СМО заявки (как под обслуживанием, так и в очереди), не покидают СМО, а ожидают конца ремонта. Все потоки событий не простейшие, а произвольные рекуррентные. Возможные состояния СМО:

S_0i — канал исправлен, в системе i заявок,

S_1i— канал ремонтируется, в системе i заявок (i = 0, 1, 2, 3).

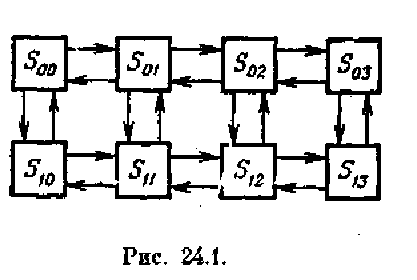Граф состояний СМО показан на рис. 24.1. Из вида графа заключаем, что финальные вероятности существуют. Предположим, что моделирование работы СМО методом Монте-Карло на большом промежутке времени Т произведено. Требуется найти характеристики эффективности СМО: Р_отк — вероятность того, что заявка покинет СМО необслуженной, Р_испр — веро­ятность того, что канал исправен, А — абсолютную пропускную способность СМО, L_сист среднее число заявок в СМО, L_оч — среднее число заявок в очереди, W_сист, и W_оч — среднее время пребывания заявки в системе и в очереди.

Сначала найдем финальные вероятности состояний p₀₀ р₀₁, р₀₂, р₀₃, p₁₀ P₁₁, P₁₂, Р₁₃. Для этого нужно вдоль реализации подсчитать суммарное время, которое система находится в каждом из состояний: Т₀₀, T₀₁, Т₀₂, Т₀₃, Т₁₀, Т₁₁, Т₁₂, Т₁₃, и разделить каждое из них на время Т. Получим:

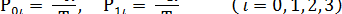
Вероятность отказа равна вероятности того, что заявка придет в момент, когда в СМО уже находятся три заявки:

Р_отк = р₀₃ + р₁₃.

Абсолютная пропускная способность равна

А=λ(1-Р_отк),

где λ — интенсивность потока заявок.

Вероятность того, что канал исправен, получим, суммируя все вероятности, у которых первый индекс равен нулю:

Р_испр = р₀₀ + р₀₁ + р₀₂ + р₀₃.

Среднее число заявок в СМО подсчитаем, умножая возможные числа заявок в СМО на соответствующие вероятности и складывая:

L_сист = 1 - (р₀₁ + р₁₁) + 2 (р₀₂ + р₁₂) + 3 (р₀₃ + p₁₃).

Это равносильно тому, как если бы мы отметили на оси времени отрезки, на которых в СМО находится 0, 1, 2, 3 заявки и суммарную длительность участков умножили соответственно на 1, 2, 3, сложили и разделили на Т.

Среднее число заявок в очереди L_оч получим, вычитая из L_сист среднее число заявок под обслуживанием (для одноканальной СМО это вероятность того, что канал занят):

Р_зап = 1 — (р₀₀ + р₁₀).

Среднее время пребывания заявки в системе и в очереди получим по формуле Литтла:

.

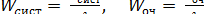На этом мы заканчиваем краткое изложение метода Монте-Карло, отсылая интересующегося читателя к руководствам [6, 22], где он изложен более полно и где, в частности, рассматривается вопрос о точности статистического моделирования.