Пример 1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления
а) 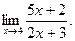
Так как 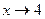 , то числитель дроби стремится к числу 5 4+2=22, а знаменатель – к числу 2 4+3=11. Следовательно, на основании теоремы 1 (предел суммы и произведения) имеем
, то числитель дроби стремится к числу 5 4+2=22, а знаменатель – к числу 2 4+3=11. Следовательно, на основании теоремы 1 (предел суммы и произведения) имеем
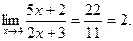
б) 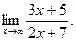
Числитель и знаменатель дроби неограниченно возрастают при 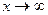 . В таком случае говорят, что имеет место неопределенность вида
. В таком случае говорят, что имеет место неопределенность вида 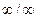 . Разделив на х числитель и знаменатель дроби, получаем
. Разделив на х числитель и знаменатель дроби, получаем
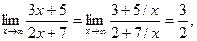
так как при 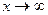 каждая из дробей 5/ x и 7/ x стремится к нулю.
каждая из дробей 5/ x и 7/ x стремится к нулю.
в) 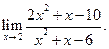
Непосредственная подстановка предельного значения аргумента х = 2 приводит к неопределенности вида 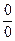 . Чтобы раскрыть эту неопределенность, разложим числитель и знаменатель на множители и сократим члены дроби на общий множитель (х – 2). Так как аргумент х только стремится к своему предельному значению 2, но не совпадает с ним, то множитель (х – 2) отличен от нуля при х ® 2:
. Чтобы раскрыть эту неопределенность, разложим числитель и знаменатель на множители и сократим члены дроби на общий множитель (х – 2). Так как аргумент х только стремится к своему предельному значению 2, но не совпадает с ним, то множитель (х – 2) отличен от нуля при х ® 2:
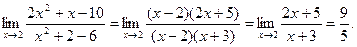
Пример 2. Найти производные первого порядка данных функций, используя правила вычисления производных
а) 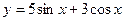
По правилу дифференцирования, производная суммы равна сумме производных и постоянный множитель можно вынести за знак производной:
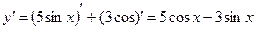 .
.
б) 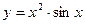
По правилу дифференцирования произведения функций находим:
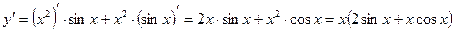
в) 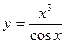
По правилу дифференцирования частного функций получаем:
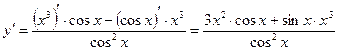 .
.
г) 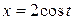 ,
,
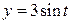
Производная функции 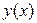 ,заданной параметрически, находится по формуле
,заданной параметрически, находится по формуле
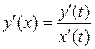 ,
,
откуда в нашем случае
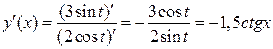 .
.
Пример 3. Построить график функции y=f(x), используя схему исследования функции 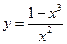 .
.
1. Область определения функции: вся числовая ось, кроме точки  .
.
2. Функция не является ни четной, ни нечетной, так как
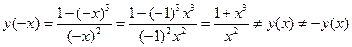 .
.
Кроме того, функция не является периодической.
3. Определим точки пересечения графика функции с осями координат.
При х = 0 функция не определена, следовательно, точек пересечения графика с осью Оy нет.
Решив уравнение у (х)=0, т. е. 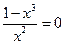 , получим точку (1; 0) пересечения с осью Oх.
, получим точку (1; 0) пересечения с осью Oх.
4. Определим точки разрыва функции. В точке  функция имеет бесконечный разрыв (второго рода):
функция имеет бесконечный разрыв (второго рода):
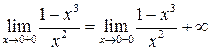 .
.
Во всех других точках числовой оси функция непрерывна.
Следовательно, х = 0 – единственная вертикальная асимптота графика функции.
5. Найдем невертикальные асимптоты графика функции.
Для этого определим коэффициенты k и b по формулам (15.2), получим:
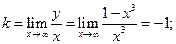
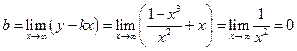 .
.
Получена наклонная асимптота 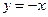 – биссектриса второго и четвертого координатных углов.
– биссектриса второго и четвертого координатных углов.
6. Для нахождения точек экстремума найдем первую производную и приравняем ее к нулю:
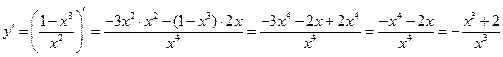
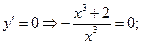
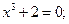
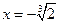 .
.
Таким образом, критические точки:
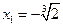 , так как в этой точке
, так как в этой точке 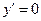 ;
;
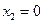 , так как в этой точке
, так как в этой точке 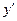 не существует (это точка разрыва).
не существует (это точка разрыва).
Рассмотрим критические точки и найдем промежутки монотонности функции:
| x | (–¥; 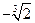 ) )
| 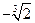
| (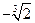 ; 0) ; 0)
| (0; +¥) | |
| y¢ | – | + | не существует | – | |
| y | 
| 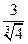 min
min
| 
| не существует | 
|
Отметим: точка 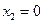 не является точкой экстремума, так как она есть точка разрыва.
не является точкой экстремума, так как она есть точка разрыва.
Точка 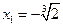 является точкой минимума, при этом
является точкой минимума, при этом
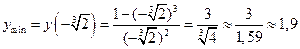 .
.
7. Для нахождения точек перегиба найдем вторую производную и приравняем ее к нулю:
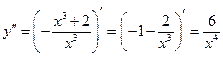 ;
; 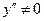 ,
, 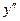 не существует при х =0,
не существует при х =0,
но это значение x не может быть абсциссой точки перегиба, так как оно является точкой разрыва. Следовательно, график функции не имеет точек перегиба. На всей области определения функции 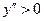 , поэтому ее график всюду вогнутый.
, поэтому ее график всюду вогнутый.
8. График функции имеет вид

Пример 4. Найти неопределенные интегралы.
а) 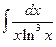
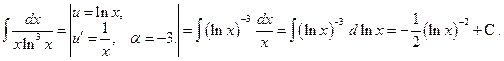
б) 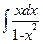
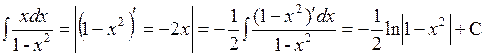 .
.
в)
Пример 5. Вычислить определенный интеграл
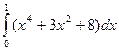
По формуле Ньютона – Лейбница:
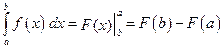 ,
,
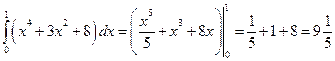
 2015-10-13
2015-10-13 273
273






