Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей

Пусть заданы две плоскости Q₁ и Q₂:

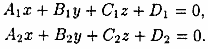
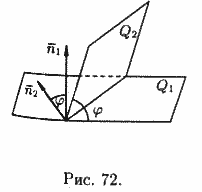
Под углом между плоскостями Q₁ и Q₂ понимается один из двугран­ных углов, образованных этими плоскостями.

Угол j между нормальными векторам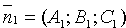и и 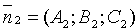плоскостей Q₁ и Q₂равен одному из этих углов (см. рис. 72).

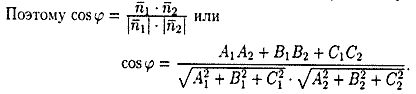
Для нахождения острого угла следует взять модуль правой части.

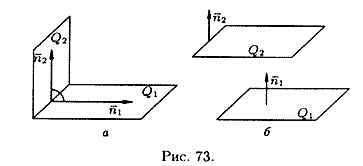
Если плоскости Q₁ и Q₂ перпендикулярны (см. рис. 73, а), то таковы же их нормали, т. е. 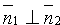(и наоборот). Но тогда 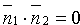, т. е. 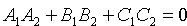. Полученное равенство есть условие перпендикулярности двух плоскостей Q₁ и Q₂.

Если плоскости Q₁ и Q₂ параллельны (см. рис. 73, б), то будут параллельны и их нормал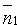и и 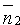(и наоборот). Но тогда, как известно координаты векторов пропорциональны: 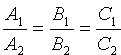. Это и есть уcловиє параллельности двух плоскостей Q₁ и Q₂.