Пусть прямые L1 и L2 заданы каноническими уравнениями
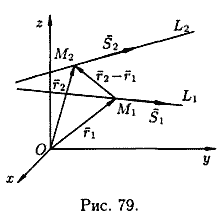
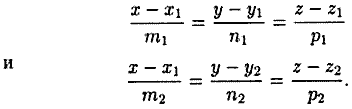
Их направляющие векторы соответственно 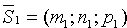 и
и 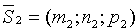 (см. рис. 79).
(см. рис. 79).
Прямая L1 проходит через точку 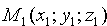 радиус-вектор которой обозначим через
радиус-вектор которой обозначим через 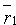 ; прямая L2 проходит через точку
; прямая L2 проходит через точку 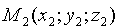 , радиус-вектор которой обозначим через
, радиус-вектор которой обозначим через 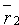 . Тогда
. Тогда
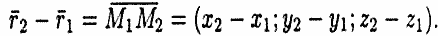
Прямые L1 и L2 лежат в одной плоскости, если векторы 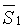 ,
, 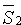 и
и 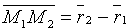 компланарны. Условием компланарности векторов являтся равенство нулю их смешанного произведения:
компланарны. Условием компланарности векторов являтся равенство нулю их смешанного произведения: 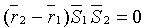 , т. е.
, т. е.
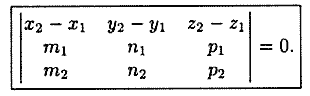
При выполнении этого условия прямые L1 и L2 лежат в одной плоскости, то есть либо пересекаются, если 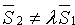 , либо параллельны, если
, либо параллельны, если 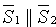 .
.
 2015-10-13
2015-10-13 9214
9214








