2015-10-13
541
Будем рассматривать стационарный процесс. Пусть внешние условия таковы, что если бы нагрева (или охлаждения) не было, то жидкость покоилась бы, имея исходную температуру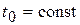 
, и плотность 
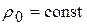. При этом распределение давления 
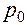в жидкости было бы гидростатическим с градиентом
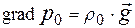. (1)
Сжимаемостью жидкости в случае свободной конвекции можно пренебрегать, считая, что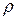 
не зависит от 
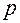. Но зависимость 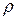от температуры 
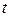как раз определяет свободную конвекцию, примем её линейной
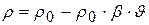, (2)
где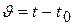 
– избыточная температура, 
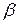– коэффициент температурного объёмного расширения, 
.
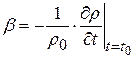Уравнение движения возьмём в прежнем виде (К4)
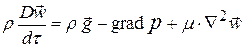. (3)
В этом уравнении слагаемые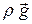 
и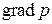 
много больше остальных, но они близки по величине, их разность мала и имеет тот же порядок, что остальные слагаемые. Это нужно использовать. Введём возмущение давления 
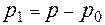, то есть
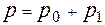, (4)
и рассмотрим указанную разность с подстановкой (2), (4) и, затем, (1):
.
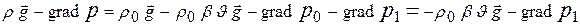Подставим это снова в (3), разделив всё уравнение на 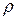(с учётом 
):
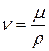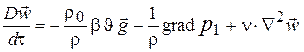. (5)
Теперь все слагаемые имеют одинаковый порядок и уже описывают механизм движения при свободной конвекции. При этом 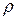очень близко к 
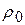, поэтому их можно далее не различать (опуская индекс 0). Кроме того, в уравнении осталось только 
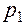(без 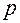), и далее будем опускать у него индекс 1, понимая под 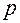возмущение давления.
|
|
|
Если учитывать, что вектор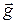 
имеет проекцию только на ось 
(
, 
, 
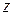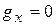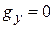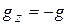), можно увидеть, что в проекции на оси уравнения движения имеют прежнюю форму (К5), кроме проекции уравнения на ось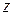
, где отличие только в первом слагаемом правой части.
После перехода к прежним (как перед (К10)) безразмерным переменным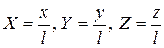 
, 
, 
, (
, 
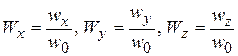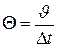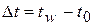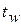– температура стенки), получим
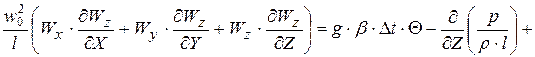
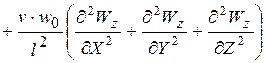, или, по аналогии с (К11)
.
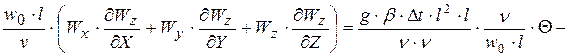
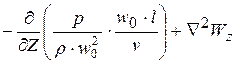Здесь, по сравнению с (К11), кроме прежних чисел подобия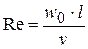 
(число Рейнольдса) и 
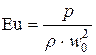(число Эйлера) появилось новое число подобия 
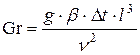– число Грасгофа.
Число Gr характеризует влияние сил, связанных с температурными возмущениями плотности (точнее, удельного веса) по сравнению с силами вязкости.
При расчётах число Gr обычно является определяющим, то есть критерием подобия (вместе с Pr). Следует отметить, что в случае свободной конвекции нет заданной скорости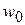 
, поэтому число Re является не заданным, а искомым, наряду с числами Nu и Eu.
Таким образом, в простых схемах с одним определяющим размером (вертикальная поверхность высотой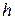 
, длинная горизонтальная труба диаметром 
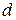) уравнение подобия для теплоотдачи должно иметь вид
.
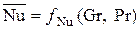В более сложных схемах, вообще говоря, могли бы добавляться параметры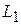 
, 
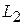и т.д., характеризующие геометрию области. А в практических уравнениях – поправочные коэффициенты. В реальных уравнениях подобия для обычных сред основным определяющим фактором оказывается произведение 
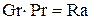– число Релея (Rayleigh), а не два отдельных числа Gr и Pr. Практические уравнения подобия стараются представить в степенной форме, так что типичная форма уравнения подобия для свободной конвекции имеет вид
|
|
|
,
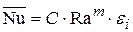где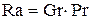 
, 
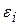– поправочные коэффициенты (один или несколько). Впрочем, при более точном рассмотрении зависимость от числа Pr учитывается отдельным множителем, так что уравнение подобия имеет структуру
.
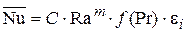Можно ещё добавить, что в типичных схемах, как оказалось, при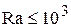 
свободная конвекция не проявляется, и имеет место чистая теплопроводность в покоящейся жидкости.
