1. При температуре 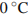 рельс имеет длину
рельс имеет длину 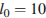 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону
м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону 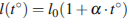 , где
, где 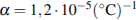 — коэффициент теплового расширения,
— коэффициент теплового расширения, 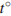 — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.
— температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.
2. Высота над землeй подброшенного вверх мяча меняется по закону 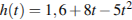 , где
, где 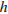 – высота в метрах,
– высота в метрах,  – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трeх метров?
– время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трeх метров?
3. В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону 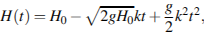 где
где  – время в секундах, прошедшее с момента открытия крана,
– время в секундах, прошедшее с момента открытия крана, 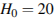 – начальная высота столба воды,
– начальная высота столба воды, 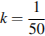 – отношение площадей поперечных сечений крана и бака, а
– отношение площадей поперечных сечений крана и бака, а  – ускорение свободного падения (считайте
– ускорение свободного падения (считайте 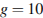 м/с
м/с  ). Через сколько секунд после открытия крана в баке останется четверть первоначального объeма воды?
). Через сколько секунд после открытия крана в баке останется четверть первоначального объeма воды?
4. Деталью некоторого прибора является вращающаяся катушка. Она состоит из трeх однородных соосных цилиндров: центрального массой 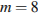 кг и радиуса
кг и радиуса 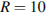 см, и двух боковых с массами
см, и двух боковых с массами 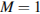 кг и с радиусами
кг и с радиусами 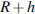 . При этом момент инерции катушки относительно оси вращения, выражаемый в
. При этом момент инерции катушки относительно оси вращения, выражаемый в 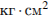 , даeтся формулой
, даeтся формулой 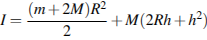 . При каком максимальном значении
. При каком максимальном значении 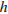 момент инерции катушки не превышает предельного значения 625
момент инерции катушки не превышает предельного значения 625 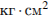 ? Ответ выразите в сантиметрах.
? Ответ выразите в сантиметрах.
5.  Для определения эффективной температуры звeзд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела
Для определения эффективной температуры звeзд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела 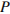 , измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвeртой степени температуры:
, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвeртой степени температуры: 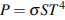 , где
, где 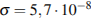 – постоянная, площадь
– постоянная, площадь 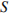 измеряется в квадратных метрах, а температура
измеряется в квадратных метрах, а температура 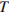 – в градусах Кельвина. Известно, что некоторая звезда имеет площадь
– в градусах Кельвина. Известно, что некоторая звезда имеет площадь 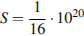 м
м  , а излучаемая ею мощность
, а излучаемая ею мощность 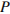 не менее
не менее 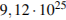 Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина.
Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина.
6. На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами.
Введём систему координат: ось Oy направим вертикально вдоль одного из пилонов, а ось Ox направим вдоль полотна моста, как показано на рисунке.
В этой системе координат линия, по которой провисает цепь моста, имеет уравнение  где x и y измеряются в метрах. Найдите длину ванты, расположенной в 30 метрах от пилона. Ответ дайте в метрах.
где x и y измеряются в метрах. Найдите длину ванты, расположенной в 30 метрах от пилона. Ответ дайте в метрах.
7. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием 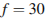 см. Расстояние
см. Расстояние 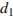 от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние
от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние 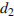 от линзы до экрана – в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение
от линзы до экрана – в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение 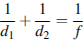 . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
8. Сила тока в цепи 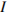 (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома:
(в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: 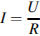 , где
, где 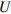 – напряжение в вольтах,
– напряжение в вольтах, 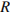 – сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в Омах.
– сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в Омах.
9. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой 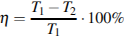 , где
, где 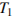 – температура нагревателя (в градусах Кельвина),
– температура нагревателя (в градусах Кельвина), 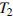 – температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя
– температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя 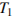 КПД этого двигателя будет не меньше
КПД этого двигателя будет не меньше 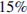 , если температура холодильника
, если температура холодильника 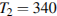 К? Ответ выразите в градусах Кельвина.
К? Ответ выразите в градусах Кельвина.
10. Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость спуска батискафа, выражаемая в м/с, определяется по формуле 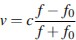 , где
, где 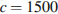 м/с – скорость звука в воде,
м/с – скорость звука в воде, 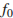 – частота испускаемых импульсов (в МГц),
– частота испускаемых импульсов (в МГц), 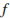 – частота отражeнного от дна сигнала, регистрируемая приeмником (в МГц). Определите наибольшую возможную частоту отраженного сигнала
– частота отражeнного от дна сигнала, регистрируемая приeмником (в МГц). Определите наибольшую возможную частоту отраженного сигнала 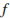 , если скорость погружения батискафа не должна превышать 2 м/с.
, если скорость погружения батискафа не должна превышать 2 м/с.
11. При движении ракеты еe видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону 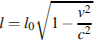 , где
, где 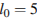 м – длина покоящейся ракеты,
м – длина покоящейся ракеты, 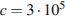 км/с – скорость света, а
км/с – скорость света, а  – скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 4 м? Ответ выразите в км/с.
– скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 4 м? Ответ выразите в км/с.
12. Уравнение процесса, в котором участвовал газ, записывается в виде 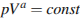 , где
, где 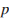 (Па) – давление в газе,
(Па) – давление в газе, 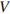 – объeм газа в кубических метрах, a – положительная константа. При каком наименьшем значении константы a уменьшение вдвое раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза?
– объeм газа в кубических метрах, a – положительная константа. При каком наименьшем значении константы a уменьшение вдвое раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза?
13. В ходе распада радиоактивного изотопа, его масса уменьшается по закону 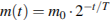 , где
, где 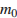 – начальная масса изотопа,
– начальная масса изотопа,  (мин) – прошедшее от начального момента время,
(мин) – прошедшее от начального момента время, 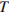 – период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени
– период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени 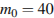 мг изотопа
мг изотопа 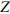 , период полураспада которого
, период полураспада которого  мин. В течение скольких минут масса изотопа будет не меньше 5 мг?
мин. В течение скольких минут масса изотопа будет не меньше 5 мг?
14. Для обогрева помещения, температура в котором равна 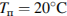 , через радиатор отопления, пропускают горячую воду температурой
, через радиатор отопления, пропускают горячую воду температурой 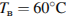 . Расход проходящей через трубу воды
. Расход проходящей через трубу воды  кг/с. Проходя по трубе расстояние
кг/с. Проходя по трубе расстояние 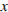 (м), вода охлаждается до температуры
(м), вода охлаждается до температуры 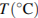 , причeм
, причeм 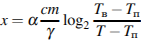 (м), где
(м), где 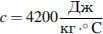 – теплоeмкость воды,
– теплоeмкость воды, 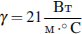 – коэффициент теплообмена, а
– коэффициент теплообмена, а 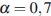 – постоянная. До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 84 м?
– постоянная. До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 84 м?
15. Небольшой мячик бросают под острым углом 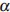 к плоской горизонтальной поверхности земли. Расстояние, которое пролетает мячик, вычисляется по формуле
к плоской горизонтальной поверхности земли. Расстояние, которое пролетает мячик, вычисляется по формуле 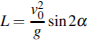 (м), где
(м), где 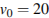 м/с – начальная скорость мячика, а
м/с – начальная скорость мячика, а  – ускорение свободного падения (считайте
– ускорение свободного падения (считайте 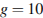 м/с
м/с  ). При каком наименьшем значении угла (в градусах) мячик перелетит реку шириной 20 м?
). При каком наименьшем значении угла (в градусах) мячик перелетит реку шириной 20 м?
16. Катер должен пересечь реку шириной 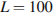 м и со скоростью течения
м и со скоростью течения 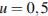 м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением
м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением 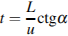 , где
, где 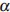 – острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом
– острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом 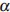 (в градусах) нужно плыть, чтобы время в пути было не больше 200 с?
(в градусах) нужно плыть, чтобы время в пути было не больше 200 с?
17. Рейтинг 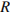 интернет-магазина вычисляется по формуле
интернет-магазина вычисляется по формуле
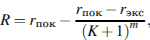
где 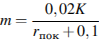 ,
, 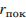 — средняя оценка магазина покупателями (от 0 до 1),
— средняя оценка магазина покупателями (от 0 до 1), 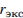 — оценка магазина экспертами (от 0 до 0,7) и
— оценка магазина экспертами (от 0 до 0,7) и 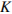 — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина «Альфа», если число покупателей, оставивших отзыв о магазине, равно 24, их средняя оценка равна 0,86, а оценка экспертов равна 0,11.
— число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина «Альфа», если число покупателей, оставивших отзыв о магазине, равно 24, их средняя оценка равна 0,86, а оценка экспертов равна 0,11.
18. Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности 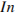 , оперативности
, оперативности 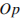 , объективности публикаций
, объективности публикаций 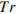 , а также качества сайта
, а также качества сайта 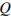 . Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от 1 до 5.
. Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от 1 до 5.
Аналитики, составляющие формулу рейтинга, считают, что объективность ценится втрое, а информативность публикаций — вдвое дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид
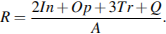
Каким должно быть число 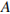 , чтобы издание, у которого все оценки наибольшие, получило бы рейтинг 1?
, чтобы издание, у которого все оценки наибольшие, получило бы рейтинг 1?
 2015-10-13
2015-10-13 610
610








