2015-10-13
211Несобственные интегралы от неограниченных функций
Пусть функция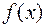 
определена и непрерывна во всех точках отрезка 
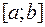за исключением точки 
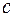, в любой окрестности которой она неограниченна. Тогда 
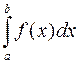не существует в обычном смысле, как предел интегральных сумм. В этом случае полагают
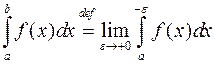при 
,
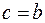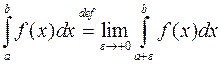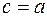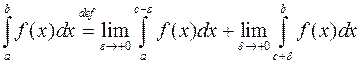при 
,
при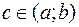 
.
Если пределы, стоящие в правых частях этих формул, существуют и конечны, то соответствующие интегралы называют сходящимися, в противном случае – расходящимися.
1. Вычислить несобственный интеграл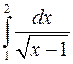 
(или доказать его расходимость).
◄ Подынтегральная функция неограниченна в любой окрестности точки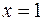 
- левого конца отрезка интегрирования (
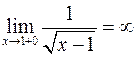). Поэтому интеграл следует понимать как несобственный:
. ►
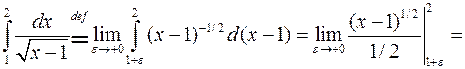
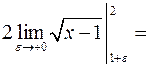
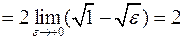2. Исследовать сходимость несобственного интеграла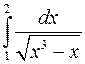 
.
◄ Как и в предыдущем примере, подынтегральная функция имеет особенность в точке 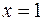. Запишем эту функцию в виде
.
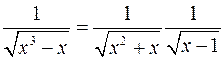Так как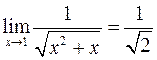 
, то 
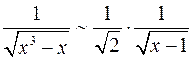при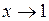 
. Согласно предыдущему примеру 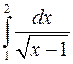сходится, следовательно, по предельному признаку сравнения сходится и .►
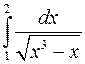3. Исследовать сходимость несобственного интеграла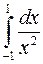 
(или доказать его расходимость).
◄ Подынтегральная функция неограниченна в любой окрестности точки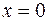 
, лежащей внутри отрезка интегрирования 
(
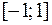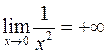). Поэтому, интеграл является несобственным.
По определению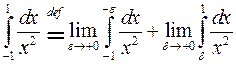 
, если конечные пределы в правой части этого равенства существуют, и 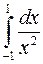расходится, если хотя бы один из этих пределов бесконечен или не существует.
Так как на самом деле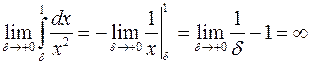 
,
то 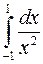- расходится. ►
